Fully coupled thermo-hydro-mechanical modelling of permeability enhancement by the finite element method
Justin Pogacnik, Department of Engineering Science
Permeability controls the percolation of fluid in porous and fractured rock and is one of the most crucial hydrologic parameters.
In geothermal systems, permeability is typically controlled by fractures and fracture connectivity within the rock mass. Because of its complexity, permeability is often a very difficult parameter to evaluate and apply in any meaningful way. This is especially true in the area of permeability enhancement. For many problems, permeability should be regarded as a time-dependent parameter, that can be enhanced or inhibited over time by various processes such as chemical species dissolution and precipitation, changes in stress or pore pressure (effective stress), and by thermo-elasto-plastic effects (thermal cracking).
Permeability often determines the feasibility of some important geologic processes and their economic potential. This is especially true in geothermal energy production. If permeability is too low, then a geothermal well is often stimulated by over pressurisation (hydrofracking or hydroshearing) or injection of cold water to induce fracturing and enhance permeability. It is the understanding of the permeability enhancement process that is the subject of my research.
We have constructed a medium description that is based on the true spatial fluctuation of material properties taken from well log and well core data, a ‘poroperm’ medium. The poroperm medium is characterised by fracture density distribution that follows a pink noise spatial fluctuation and a related long-tailed permeability distribution that describes the fracture connectivity in the medium. Small changes in fracture density result in large changes in permeability. Specifically, we are simulating fluid percolation flow and heat flow through a deformable poroperm medium using the finite element method. Due to spatial fluctuations in porosity, and thus permeability, fluids tend to percolate through native permeability pathways in the medium. The key to sustainable and productive heat extraction lies in the enhancement of those native percolation pathways to allow sufficient flow rates without allowing cold water to pass to the receiver wells. We are seeking to understand the physics of injection induced strain damage that result in permeability enhancement of the existing native permeability pathways.
Simulating finite elements
Finite element simulations were performed on the NeSI Pan cluster using my own C++ software and using LAPack++ and Magma linear-solver software. Pan allowed me to run these simulations that would otherwise not be possible with just the resources in our lab. In the finite element method, a finer mesh solves the governing partial differential equations more accurately. CPU memory is often the limiting factor for the spatial resolution of the mesh. Finer meshes create many more degrees of freedom, which consume copious amounts of random access memory (RAM). The simulations performed in my research are fully coupled multiphysics simulations. Fully coupling different partial differential equations creates an additional memory burden by increasing the size of the linear system that needs to be solved. Adding solid mechanics to a fluid and heat transport system further increases the size of the linear system by a factor of three.
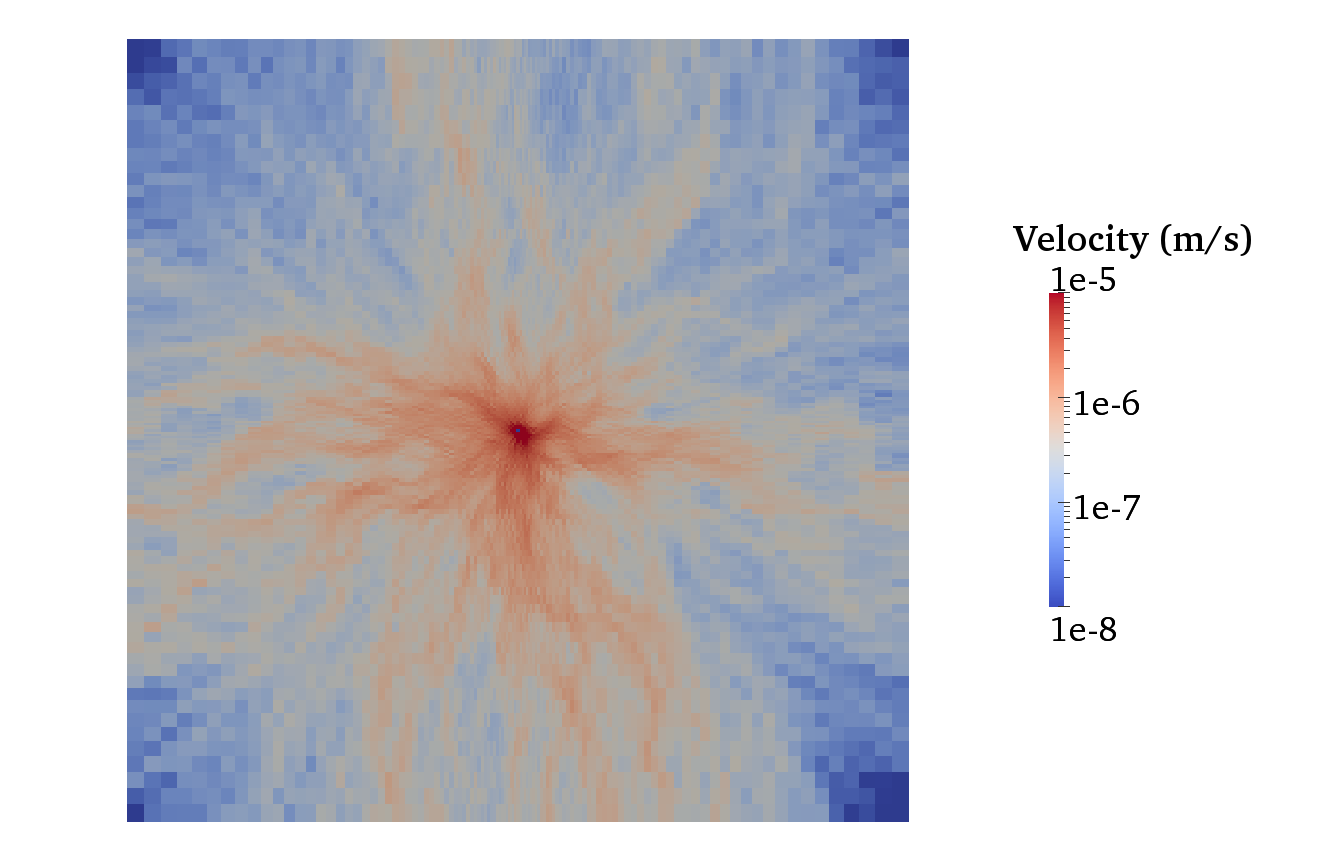
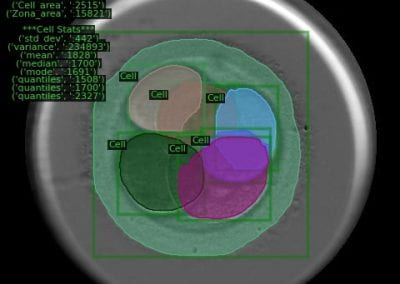
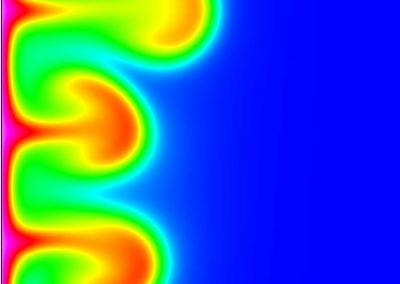
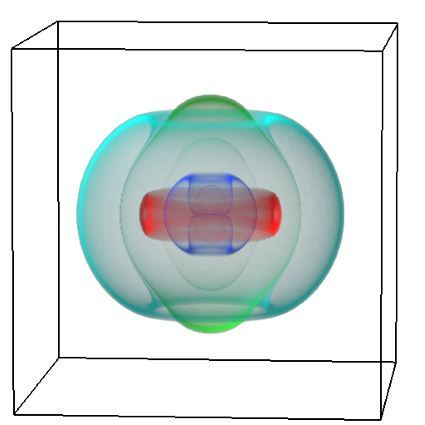
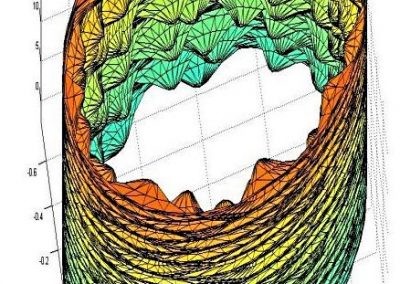
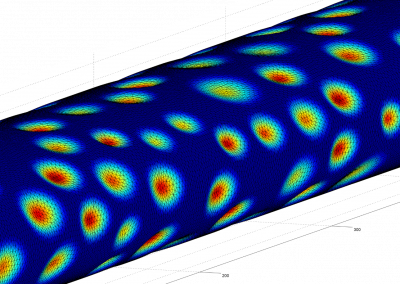
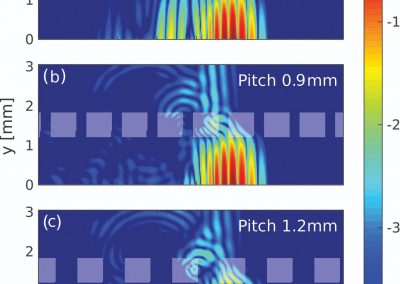
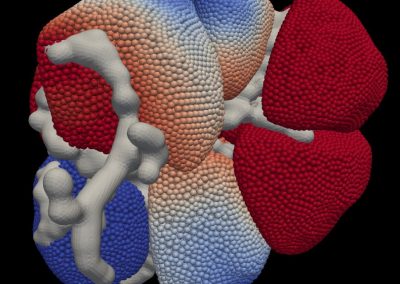
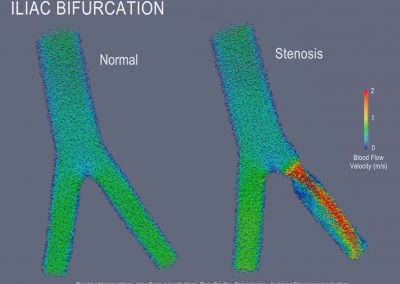
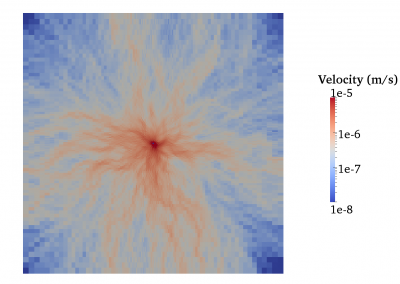
Figure 1: Vertical 2D section that shows normalised fluid velocities around an injection well. Fluids tend to percolate in native permeability pathways as a result of fracture connectivity in the rock. The goal of native permeability enhancement is to stimulate these native pathways through shear deformation and damage to increase flow rates without compromising the heat of the reservoir.
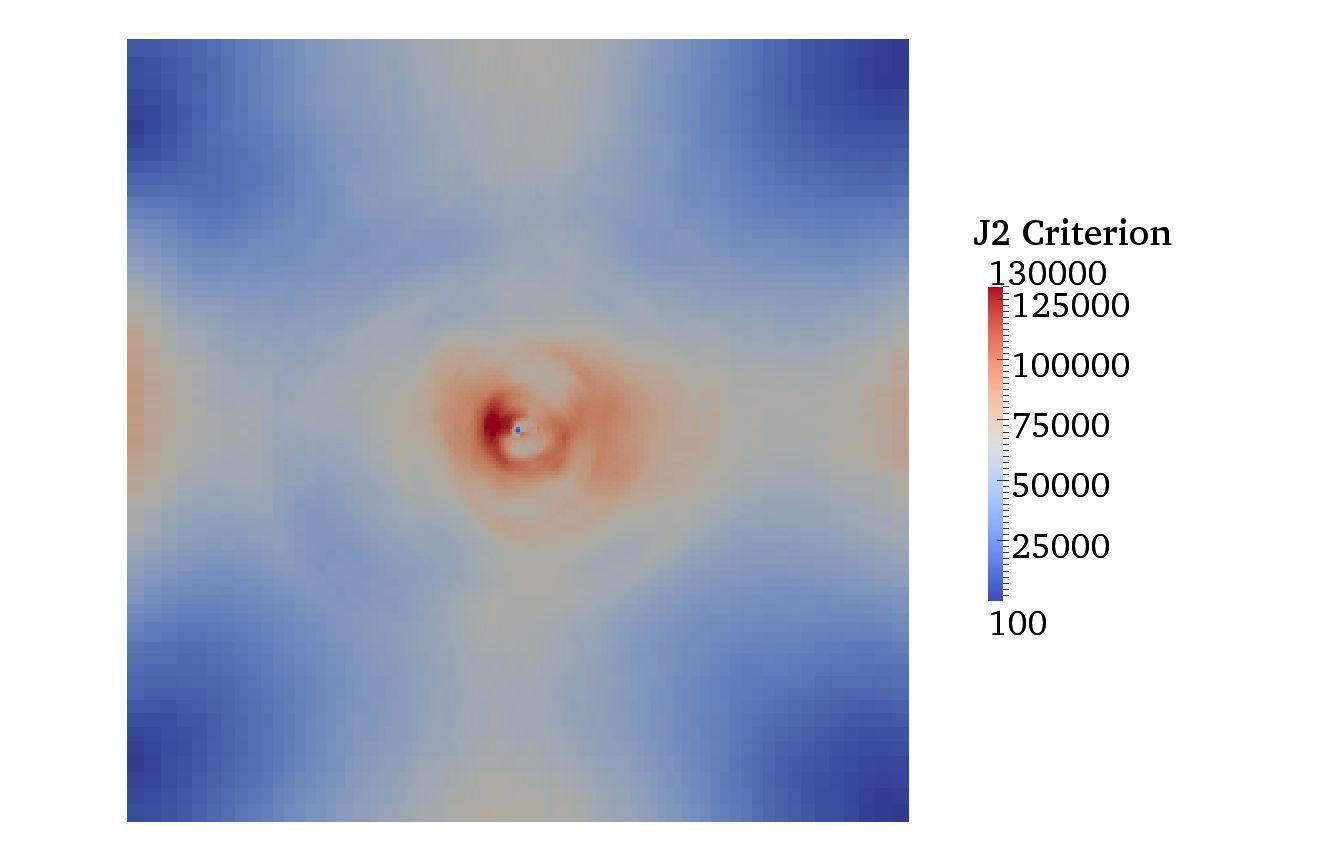
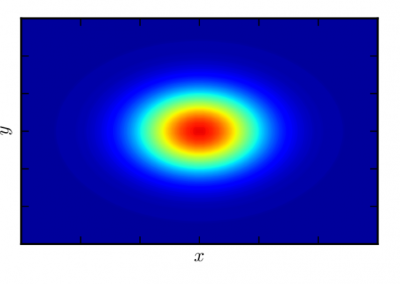
Figure 2: Von Mises J2 yield stress criterion around the injection well from Figure 1. The J2 criterion is the second principal stress invariant or the difference between the maximum and minimum principal stresses. Areas of dark red indicate the areas where the most damage and yielding are likely to occur due to stress concentrations that result from native fractures in the rock. The damage in those areas results in an increase in fracture connectivity and thus fluid flow in the percolation pathways.
The simulations shown in figures (1,2) above were performed on a single node of the NeSI cluster that included 12 cores and 96GB of RAM. Compared to my desktop computer which has 8GB of RAM, I have been able to run significantly finer grids in less time. I could not perform a finite element simulation with even half the mesh resolution of the images seen on my desktop computer.
While the initial thought of parallelising a serial code can be daunting, I found the process to be very simple using OpenMP and shared-memory parallelisation (SMP). The commands are easy to use and many linear solver packages have SMP versions that can be downloaded, compiled, and installed fairly easily. I also found the eResearch staff to be very helpful when installing necessary packages for my research. I’m able to run simulations with much finer mesh resolution that are more accurate as a result of the NeSI Pan cluster.
See more case study projects

Our Voices: using innovative techniques to collect, analyse and amplify the lived experiences of young people in Aotearoa
Painting the brain: multiplexed tissue labelling of human brain tissue to facilitate discoveries in neuroanatomy

Detecting anomalous matches in professional sports: a novel approach using advanced anomaly detection techniques
Benefits of linking routine medical records to the GUiNZ longitudinal birth cohort: Childhood injury predictors
Using a virtual machine-based machine learning algorithm to obtain comprehensive behavioural information in an in vivo Alzheimer’s disease model
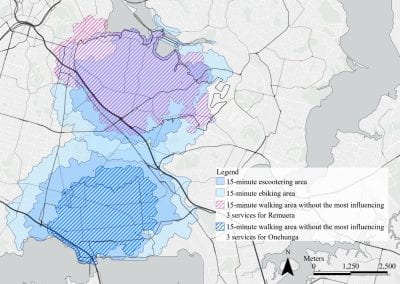
Mapping livability: the “15-minute city” concept for car-dependent districts in Auckland, New Zealand
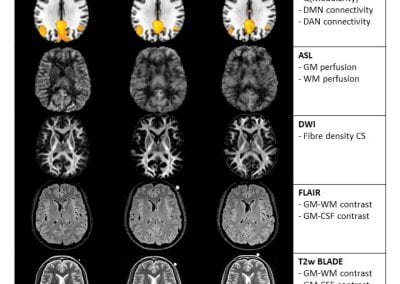
Travelling Heads – Measuring Reproducibility and Repeatability of Magnetic Resonance Imaging in Dementia
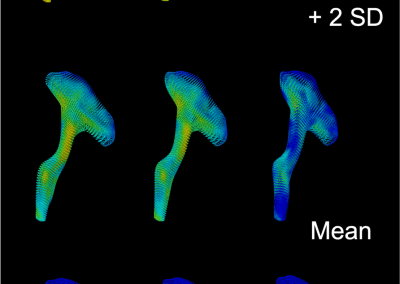
Novel Subject-Specific Method of Visualising Group Differences from Multiple DTI Metrics without Averaging

Re-assess urban spaces under COVID-19 impact: sensing Auckland social ‘hotspots’ with mobile location data
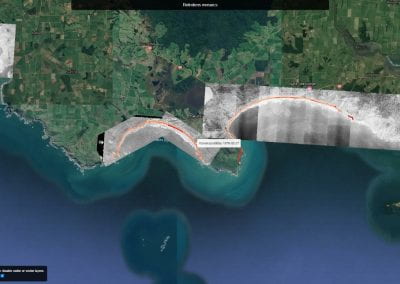
Aotearoa New Zealand’s changing coastline – Resilience to Nature’s Challenges (National Science Challenge)
Proteins under a computational microscope: designing in-silico strategies to understand and develop molecular functionalities in Life Sciences and Engineering
Coastal image classification and nalysis based on convolutional neural betworks and pattern recognition
Determinants of translation efficiency in the evolutionarily-divergent protist Trichomonas vaginalis
Measuring impact of entrepreneurship activities on students’ mindset, capabilities and entrepreneurial intentions

Using Zebra Finch data and deep learning classification to identify individual bird calls from audio recordings
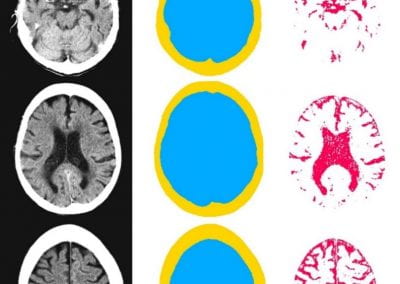
Automated measurement of intracranial cerebrospinal fluid volume and outcome after endovascular thrombectomy for ischemic stroke

Using simple models to explore complex dynamics: A case study of macomona liliana (wedge-shell) and nutrient variations
Fully coupled thermo-hydro-mechanical modelling of permeability enhancement by the finite element method

Modelling dual reflux pressure swing adsorption (DR-PSA) units for gas separation in natural gas processing
Molecular phylogenetics uses genetic data to reconstruct the evolutionary history of individuals, populations or species
Wandering around the molecular landscape: embracing virtual reality as a research showcasing outreach and teaching tool