Homodynamics in the microcirculation
Tet Chuan Lee, PhD candidate, Dr Richard John Clarke, Supervisor, Dr David Scott Long, Co-supervisor, Department of Engineering Science
Overview
The microcirculation is the network of smallest blood vessels that deliver nutrients to the body’s organs and tissues. The walls of these blood vessels (and in fact the majority of blood vessels) are coated in a structure known as the Endothelial Glycocalyx Layer (EGL). It is a porous brush-like layer that consists of many different components. The EGL is believed to serve a number of important physiological functions including the protection of the vessel walls from potentially harmful levels of fluid shear stress from the blood and as a transducer of mechanical stress from the vessel lumen. It is also hypothesised that it may play an important role in regulating vessel permeability and in the body’s inflammatory response. As such, it has received a great deal of research interest in recent years.
One of the difficulties in conducting research on the EGL is that it is extremely sensitive to changes in its environment. Some of the components that make up the EGL exist in a dynamic equilibrium with blood flow and so in-vitro experiments may degrade the EGL. In-vivo measurements are also extremely challenging, in part due to the small sizes involved in the microcirculation. As such, this work seeks to develop computational models that will enable us to better understand the EGL and its roles in the microcirculation.
Previous models have generally assumed an idealised geometry such as a vessel with a circular cross-section or have worked in two dimensions. A physiologically realistic microvessel, however, is unlikely to be circular. Instead, it will have an undulating shape due to the presence of the endothelial cells that make up its surface. These endothelial cells will protrude into the vessel due to their cell nuclei. The EGL itself is also believed to have a non-uniform distribution along the vessel surface. In fact, it has been hypothesised that the EGL redistributes to the cell-cell junctions where the endothelial cell height is lowest in order to minimise the shear stress experienced at the surface of the vessel.
In order to investigate this, a computation model for an EGL lined microvessel was developed using the Boundary Element Method. In this model, the EGL was treated using volume-average Biphasic Mixture Theory equations. In Biphasic Mixture Theory, the EGL is made up of two components, the solid fraction, which is taken to be the glycocalyx and a fluid fraction which is the blood that flows through the porous EGL. The model was developed to allow the simulation of an arbitrary vessel shape and EGL distribution in three dimensions.
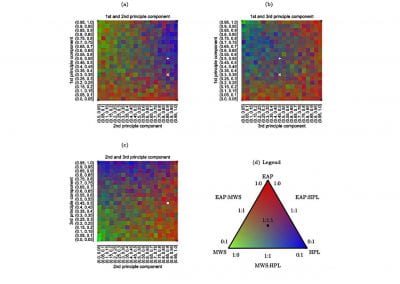
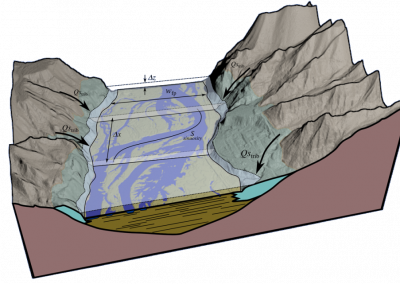
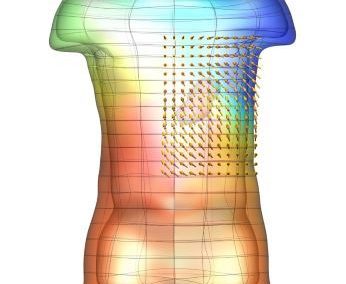
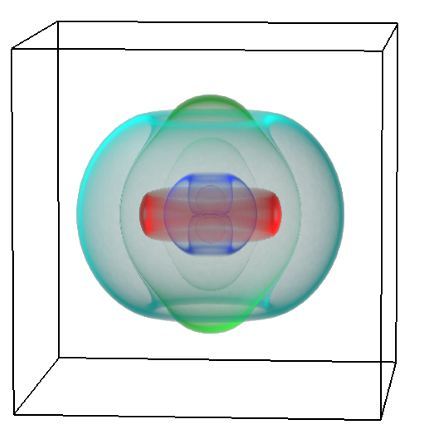
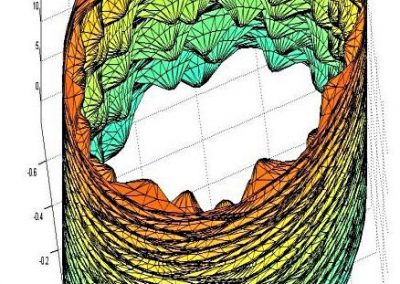
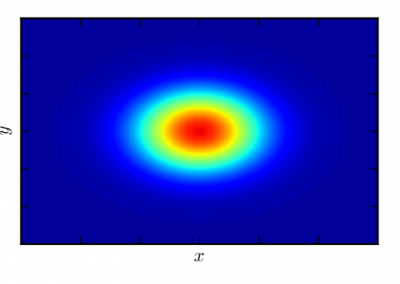
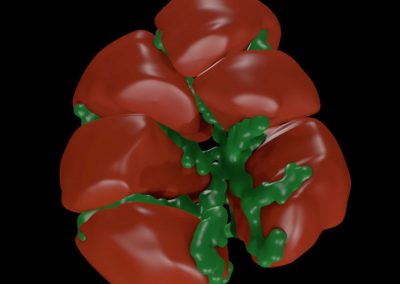
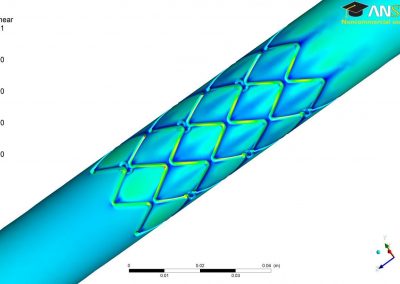
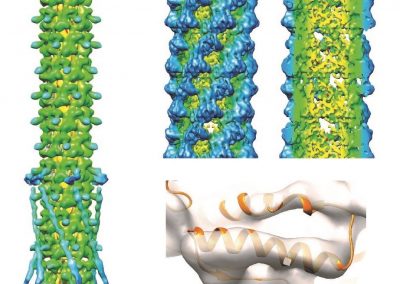
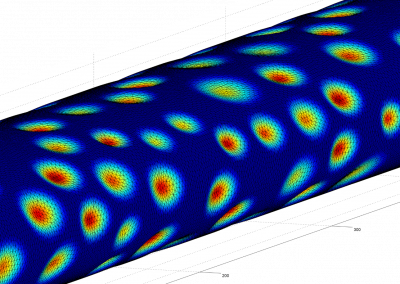
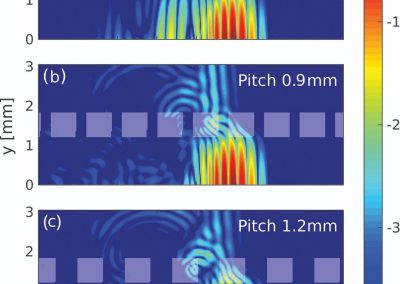
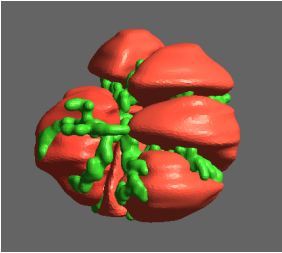
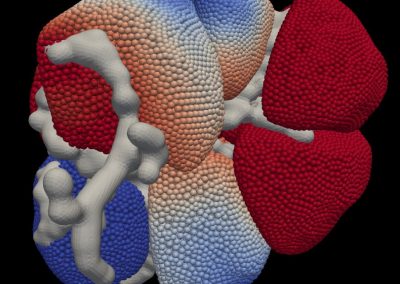
A more physiologically realistic vessel geometry was then constructed (Figure 1), informed by Confocal Microscopy Images of a post-capillary venule. The flow through the vessel was then simulated with different prescribed distributions of the EGL. This allowed us to compare vessels with an EGL that is uniformly distributed and one where it has been redistributed to the cell-cell junctions and found that the redistribution of the EGL does indeed appear to reduce the shear stress experienced by the vessel walls as seen in Figure 2.
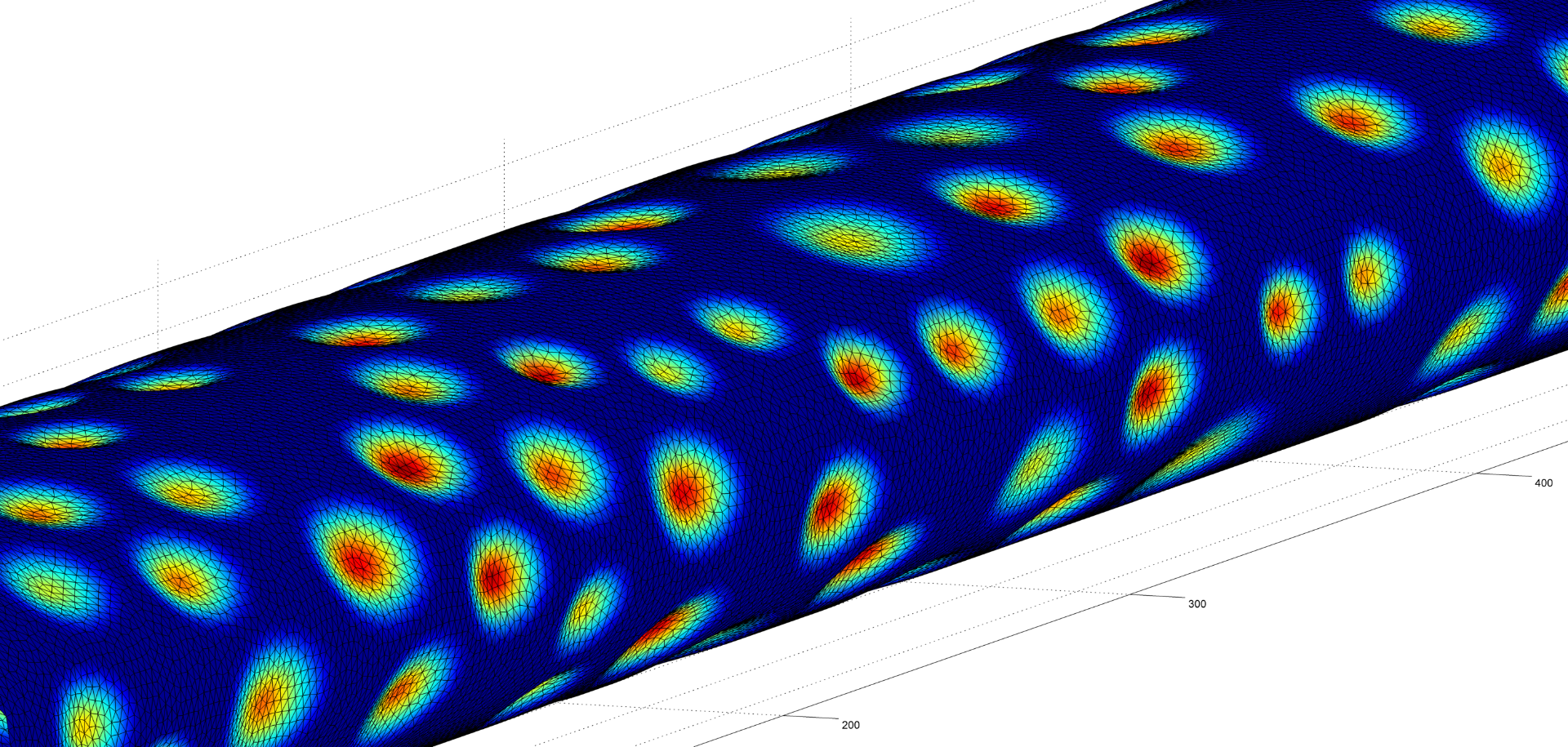
Figure 1 – A computational mesh of a microvessel used in these simulations. The undulating shape is due to the endothelial cells that make up its surface (colour rendering indicates height).
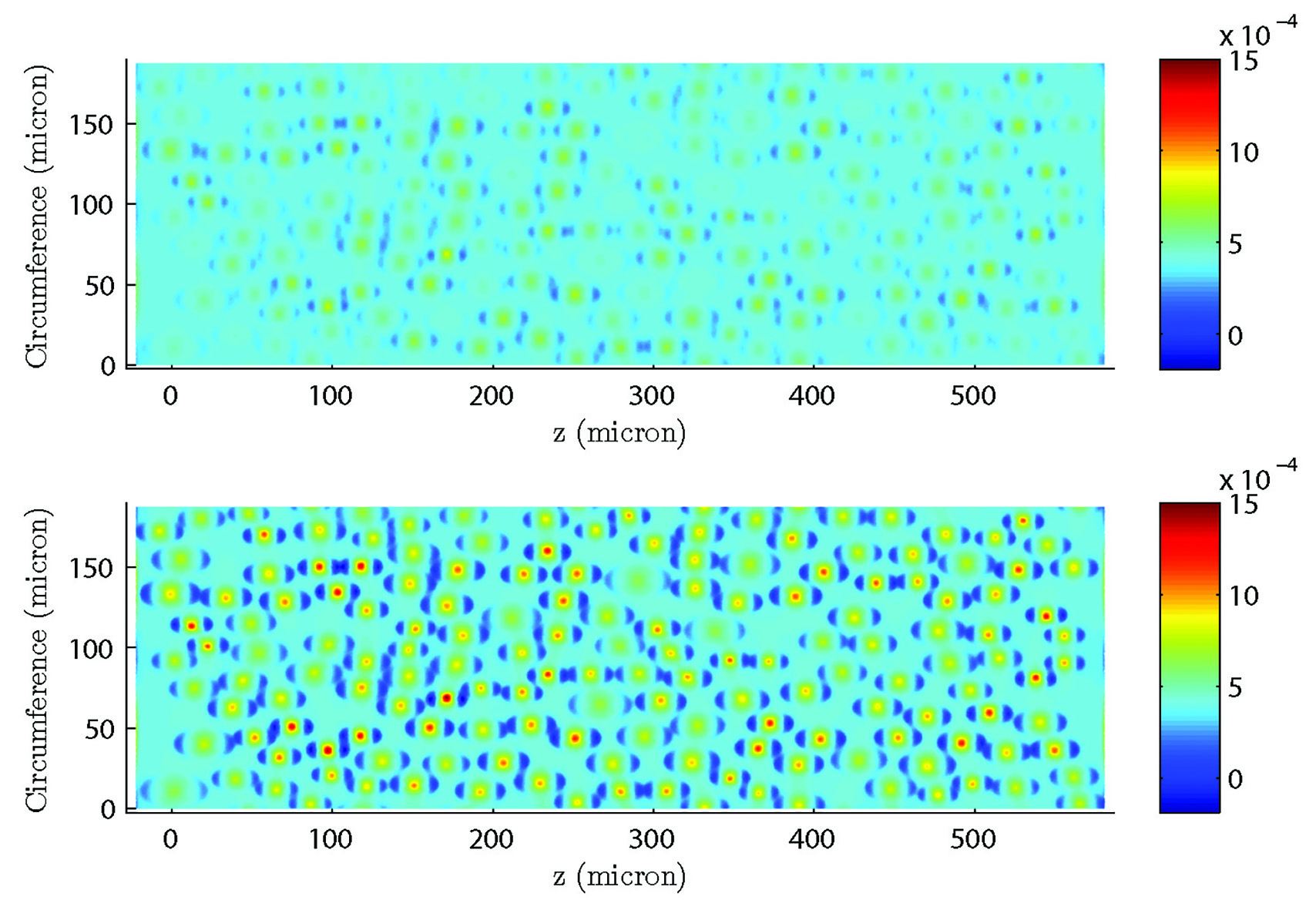
Figure 2 – Results from a simulation comparing a redistributed EGL (top) to one with a uniform distribution (bottom). As can be seen from the plots, the redistributed EGL experiences much less fluid shear stress than the one with a uniformly distributed EGL.
Computational resources
In order to perform simulations on the physiologically realistic vessel that has been created, a mesh fine enough to resolve the endothelial cells that make up its shape is required. As the Boundary Element Method (BEM) which was used to create the computational model produces densely filled matrices, the memory requirements to undertake these simulations was substantial. The Pan cluster provides access to the computational resources that are necessary to be able to undertake simulations of a microvessel with a geometry of this complexity.
The BEM leads itself to parallelisation as each entry in matrix it produces is independent of the other entries. As such, these simulations are particularly suited to being performed on a computational cluster such as the Pan cluster. By distributing the matrix onto multiple nodes and then constructing each part of the matrix locally, the construction of the matrix is greatly sped up. This matrix is then solved using PETSc which allows the interative solution of distributed linear systems using MPI communication.
Without the computational resources provided by the Pan cluster, it would not be possible undertake these simulations due to the memory constraints of a desktop computer. Furthermore, the time taken to perform these simulations would be much greater, potentially up to hundreds of times longer. Finally, the Pan cluster allowed a greater number of simulations to be undertaken which allowed more comparisons to be made between the different distributions of the EGL.
