Listening to equations: a tool for the audification of heteroclinic networks
Professor Claire Postlethwaite Department of Mathematics; Dr Nelis Drost, Senior Specialist, Centre for eResearch
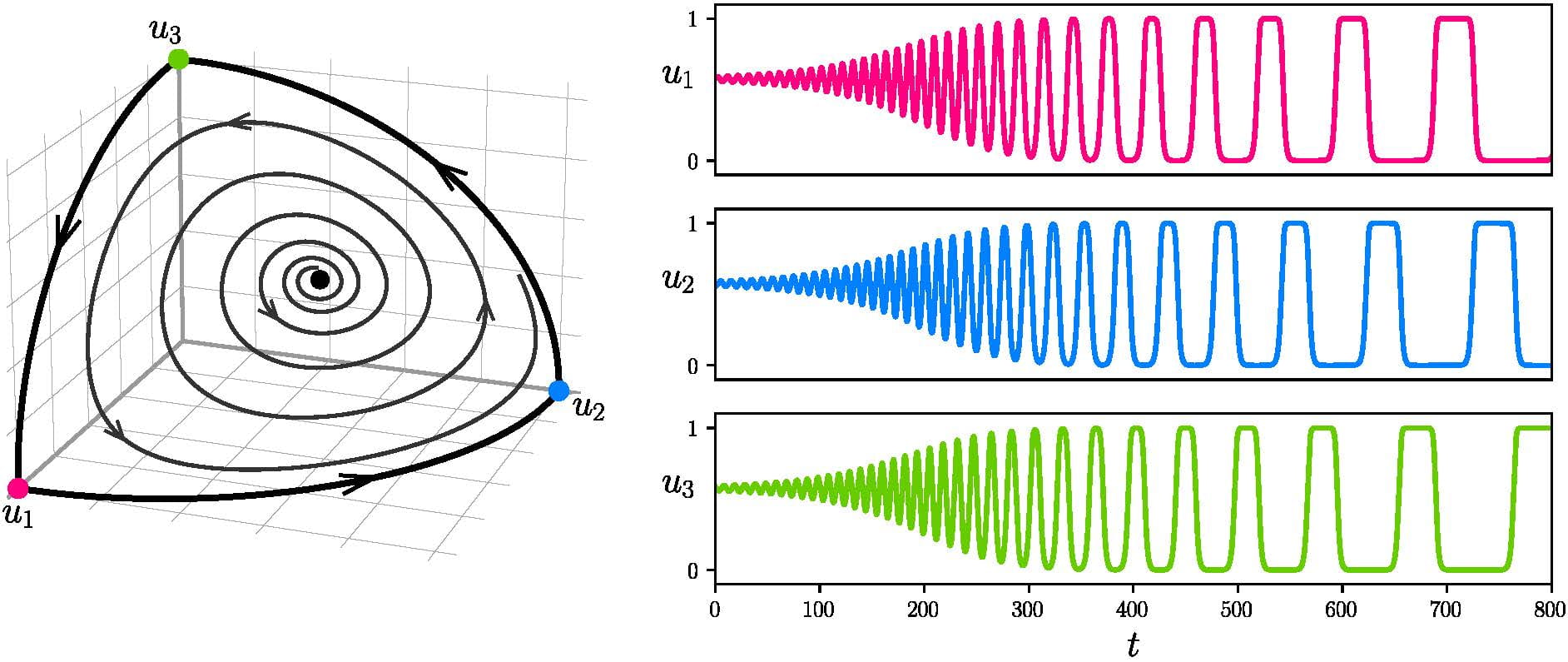
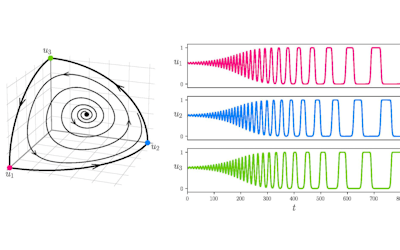
Figure 1. The switching between states eventually slows down: the period of the oscillations is not constant, but lengthens over time.
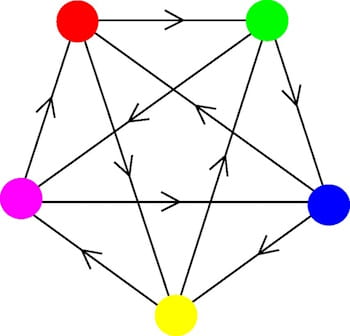
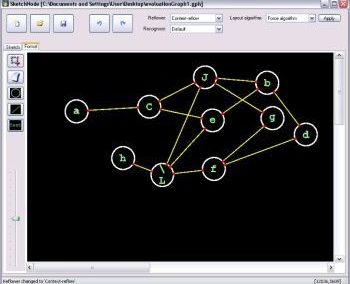
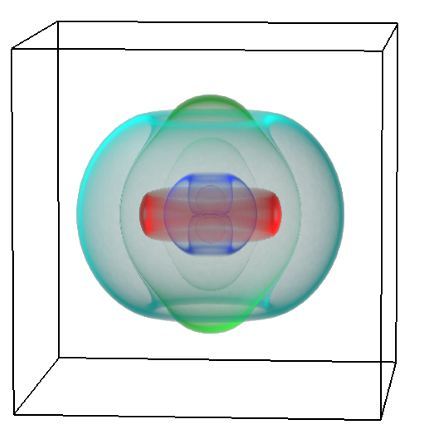
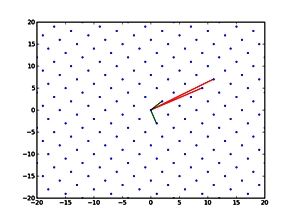
Figure 2. Heteroclinic networks are collections of heteroclinic cycles.
Because the period of the oscillations in the time-series gradually increases, or in other words, the frequency decreases, the pitch of the sound you hear decreases. Interestingly, it can be shown mathematically that the frequency decreases geometrically with time, and this has the effect that the pitch of the note you hear seems to decrease in a linear fashion: as if you were moving your hand down the notes of a piano at a constant speed. In addition, as time progresses, the oscillations change in shape from sinusoidal to square waves; this causes the change in timbre you can hear from the pure tone of the sinusoidal to the harsher sound of the square wave.
The pitch again decreases, but not so steadily; there are discontinuous jumps in both volume and pitch as the trajectory switches between different parts of the network.
See more case study projects

Our Voices: using innovative techniques to collect, analyse and amplify the lived experiences of young people in Aotearoa
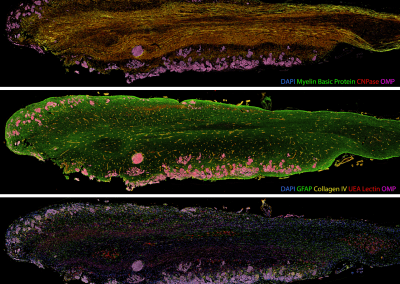
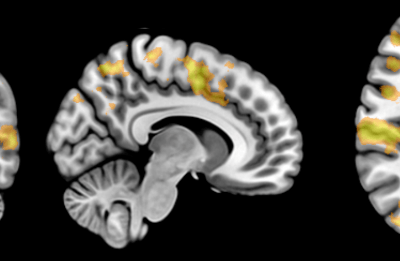
Painting the brain: multiplexed tissue labelling of human brain tissue to facilitate discoveries in neuroanatomy

Detecting anomalous matches in professional sports: a novel approach using advanced anomaly detection techniques
Benefits of linking routine medical records to the GUiNZ longitudinal birth cohort: Childhood injury predictors
Using a virtual machine-based machine learning algorithm to obtain comprehensive behavioural information in an in vivo Alzheimer’s disease model
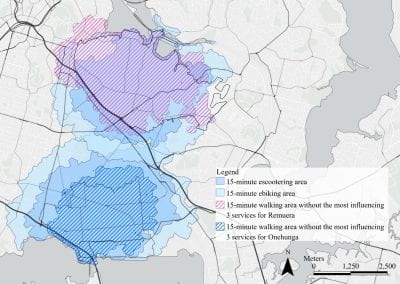
Mapping livability: the “15-minute city” concept for car-dependent districts in Auckland, New Zealand
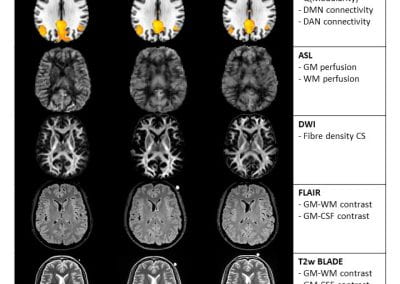
Travelling Heads – Measuring Reproducibility and Repeatability of Magnetic Resonance Imaging in Dementia
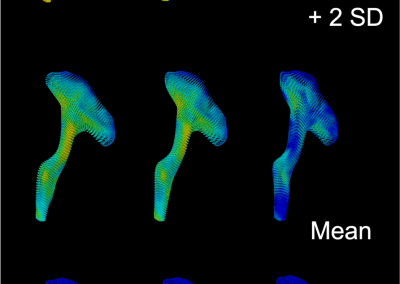
Novel Subject-Specific Method of Visualising Group Differences from Multiple DTI Metrics without Averaging

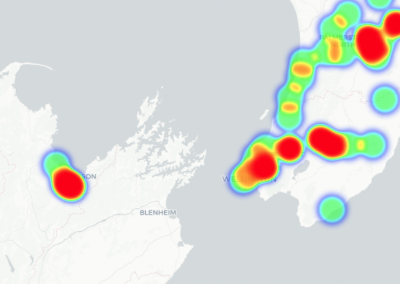
Re-assess urban spaces under COVID-19 impact: sensing Auckland social ‘hotspots’ with mobile location data
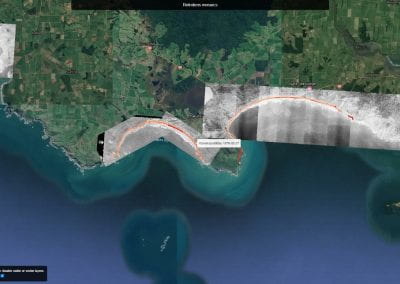
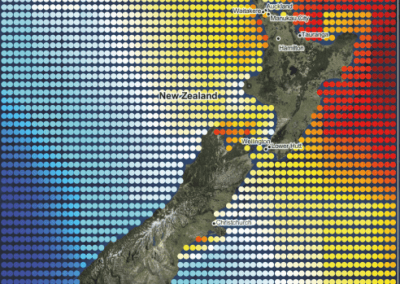
Aotearoa New Zealand’s changing coastline – Resilience to Nature’s Challenges (National Science Challenge)
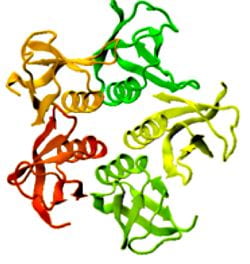
Proteins under a computational microscope: designing in-silico strategies to understand and develop molecular functionalities in Life Sciences and Engineering
Coastal image classification and nalysis based on convolutional neural betworks and pattern recognition
Determinants of translation efficiency in the evolutionarily-divergent protist Trichomonas vaginalis
Measuring impact of entrepreneurship activities on students’ mindset, capabilities and entrepreneurial intentions

Using Zebra Finch data and deep learning classification to identify individual bird calls from audio recordings
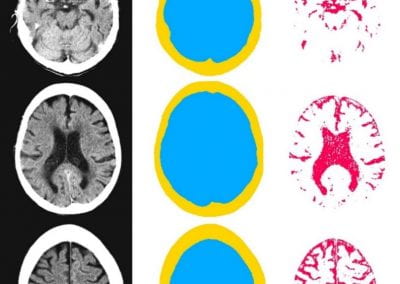
Automated measurement of intracranial cerebrospinal fluid volume and outcome after endovascular thrombectomy for ischemic stroke

Using simple models to explore complex dynamics: A case study of macomona liliana (wedge-shell) and nutrient variations
Fully coupled thermo-hydro-mechanical modelling of permeability enhancement by the finite element method

Modelling dual reflux pressure swing adsorption (DR-PSA) units for gas separation in natural gas processing
Molecular phylogenetics uses genetic data to reconstruct the evolutionary history of individuals, populations or species
Wandering around the molecular landscape: embracing virtual reality as a research showcasing outreach and teaching tool