Mathematically modelling gastrointestinal electrical activity
Shameer Sathar, Jerry Gao, Mark Trew, Leo Cheng, Auckland Bioengineering Institute
The gastrointestinal system
The gastrointestinal (GI) system comprises a series of discrete organs, from mouth to anus, with distinct functions – digestion, absorption of nutrients, excretion, and protection from digestive agents and pathogens.
GI motility, the regulated contraction of muscles along the GI tract, is coordinated by the underlying omnipresent electrical activity termed as slow waves. These are initiated and propagated through networks of the interstitial cells of Cajal (ICC) to the smooth muscle cells (SMC).
Gastric dysrhythmias, or abnormal electrical activity in the stomach, have been implicated in the pathophysiology of several motility disorders, such as gastroparesis. A validated mathematical model offers a virtual medium in which a variety of hypotheses can be comprehensively investigated. The effects of different treatment strategies can also be predicted, potentially more cost effectively than by other experimental approaches.
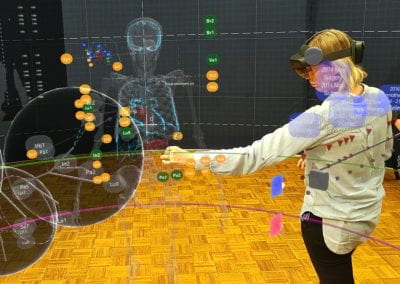
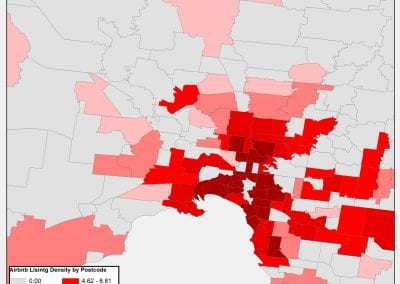
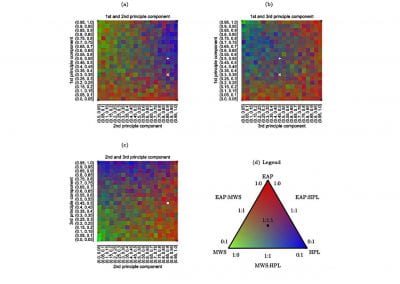
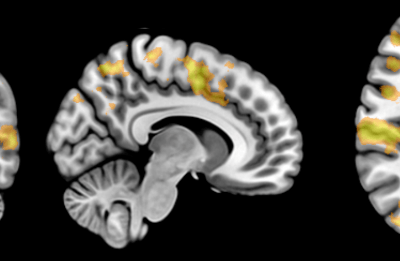
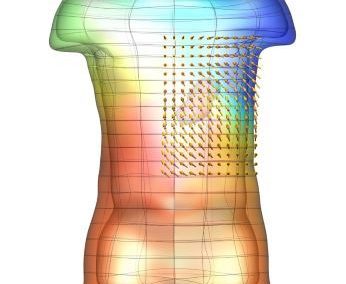
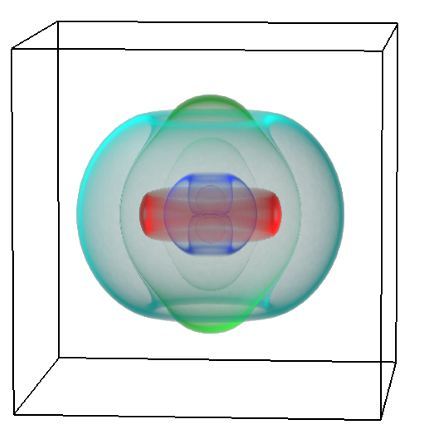
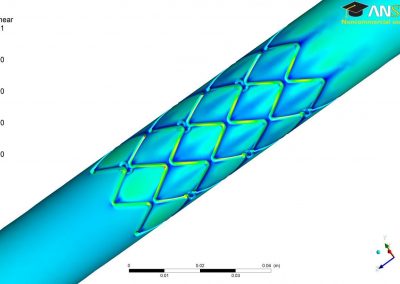
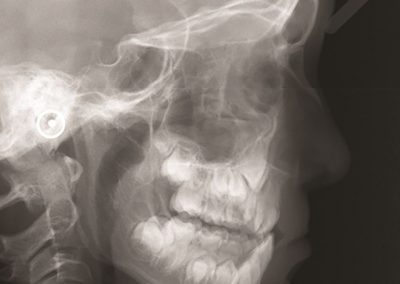
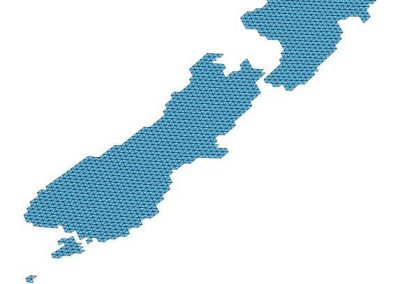
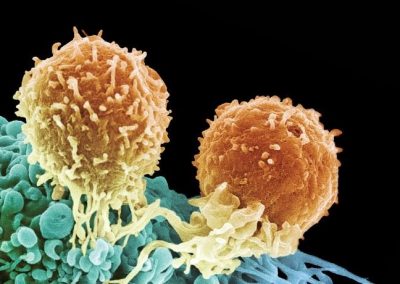
An exciting application, is using models to relate body surface electric field, or magnetic field, potentials to the underlying gastric slow wave activity, as shown in Figure 1. Modelling on the Pan cluster
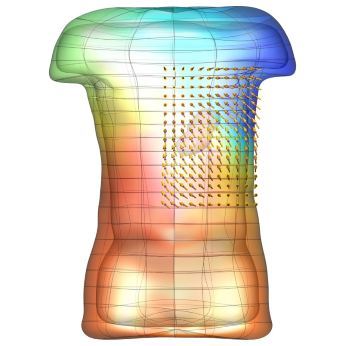
Figure 1: Torso model with electric potential fields (coloured surface) and magnetic fields (gold arrows) resulting from simulated gastric slow wave activity. Work conducted in conjunction with Prof. Alan Bradshaw (Vanderbilt University, Nashville, TN).
Modelling on the Pan cluster
Multiscale models of gastric electrophysiology (encompassing the subcellular, cell, tissue, organ, and whole-body scales) can be mathematically described by continuum modelling frameworks such as the monodomain or bidomain equations. Spatial discretisation of the 3D geometrical domain, using a finite element method, leads to a system of differential-algebraic equations. A semi-implicit method is used for temporal discretisation, where the linear term is treated implicitly and the nonlinear terms explicitly. The numerical solution of these equations on tissue-specific geometric models is typically computationally expensive. The CHASTE computational package, originally developed by the Computational Biology Group at the University of Oxford for solving tissue electrophysiology problems with cardiac applications, is being used for this research. It is built upon an MPI-based library, enabling it to efficiently split the high computational demands of simulation over many parallel processes. The CHASTE code scales linearly across multiple cores of the NeSI Pan cluster.
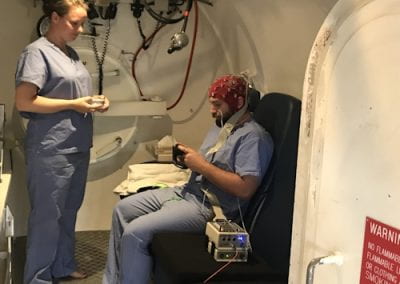
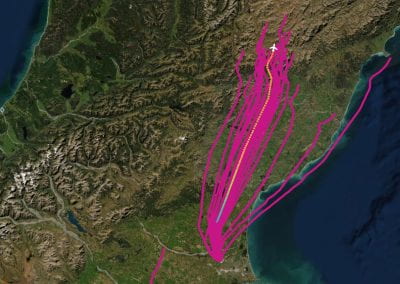
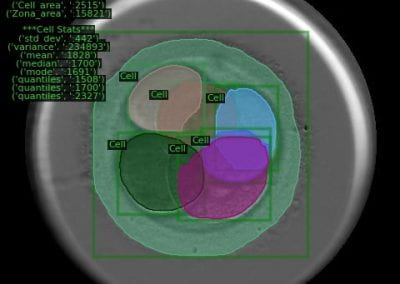
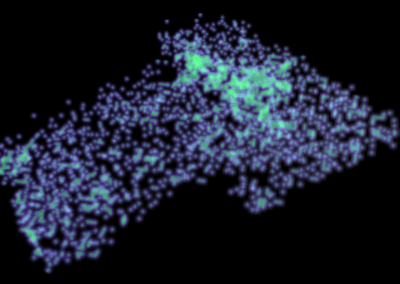
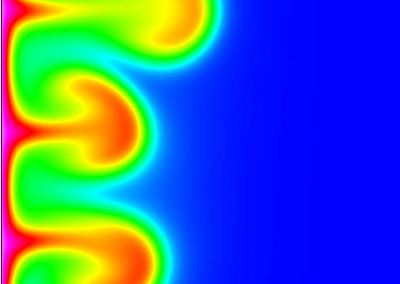
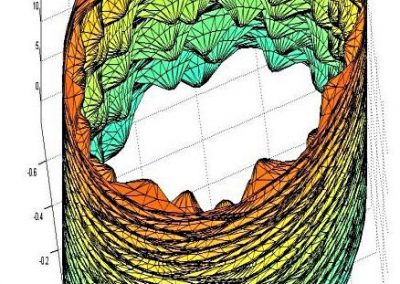
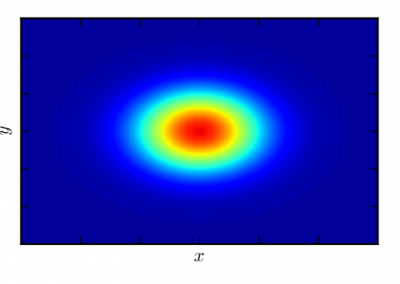
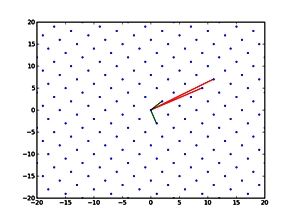
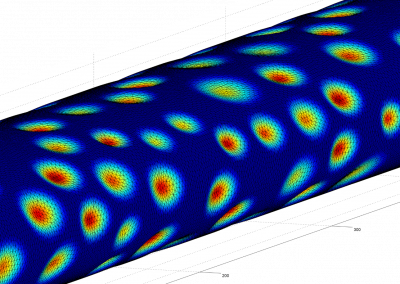
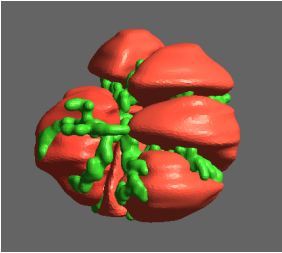
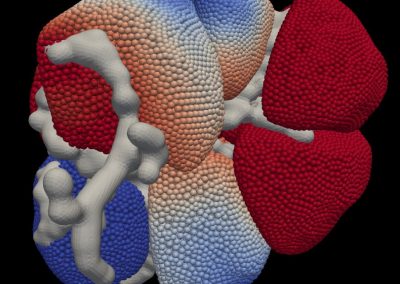
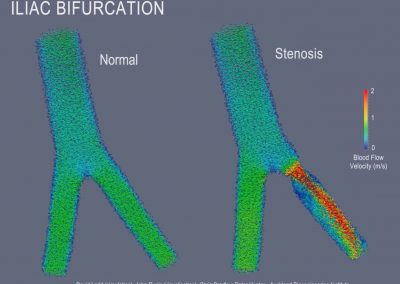
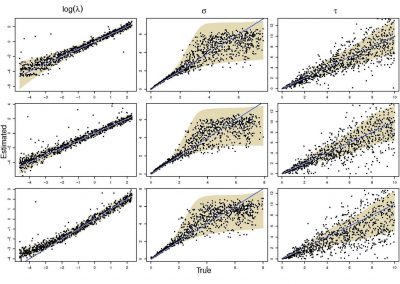
Recently, we developed a mathematical model for quantifying ICC network-function relationships by embedding biophysically-based ICC cell models into tissue-specific ICC network imaging data. Figure 2 shows the activation-time map of slow waves over an ICC network. This particular problem was relatively small, with about 300,000 solution points and a simulation time of 1000 ms. However, multiple sets of ICC network samples were analysed in parallel, as multiple independent jobs, each using up to 32 cores. The entire set of ICC networks were fully analysed in less than 48 hours using the cluster. If the NeSI Pan cluster had not been available, this data may have required weeks for analysis.
Figure 2. Slow wave simulation over an ICC network. (a) Tissue-specific ICC network imaging data. (b) Activation time map of slow waves over the network.
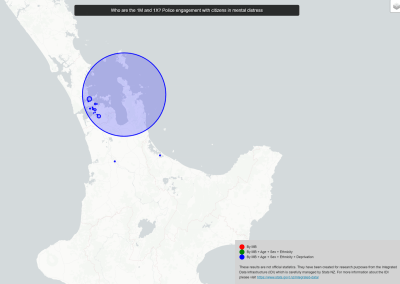
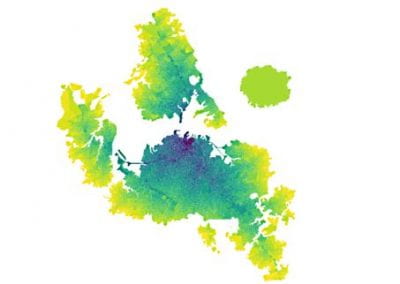
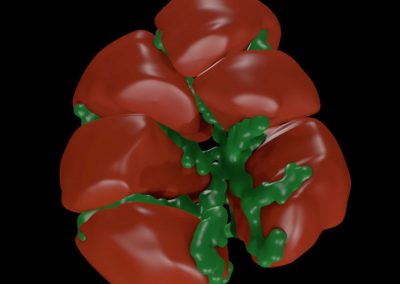
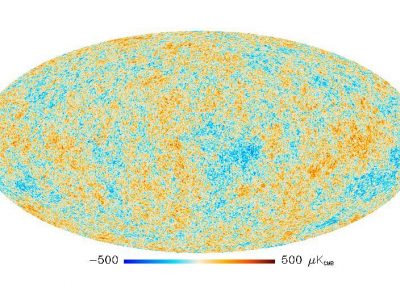
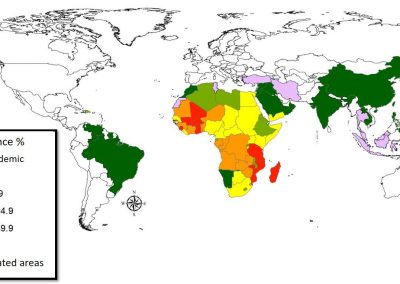
Figure 3. Simulated slow wave activity on an anatomically realistic stomach geometry.
What next?
In the future, we plan to simulate gastric electrophysiology on a 3D computational domain (approximately 3 million computational nodes) over temporal durations of up to several minutes. This model will incorporate recently developed, biophysically based, ICC and SMC cell models, along with analysed ICC network function data. We aim to simultaneously utilise up to 1024 cores of the NeSI Pan cluster and concurrently employ the cluster GPU resources. Figure 3 shows preliminary results for slow wave simulations in the stomach.
