Novel Subject-Specific Method of Visualising Group Differences from Multiple DTI Metrics without Averaging

Eryn E Kwon^1,2,3, Maryam Tayebi^1,3, Joshua McGeown^1,2, Matthew McDonald^1,2, Patrick McHugh1,4, Paul Condron^1,2, LeighPotter^1,5, Davidson Taylor^1,6, Jerome Maller⁷, Miao Qiao8, Alan Wang^1,2,3, Poul Nielsen^3,8, Justin Fernandez^1,3,8, Miriam Scadeng^1,2, Samantha Holdsworth^1,2, and Vickie Shim^1,3.

¹ Mātai Medical Research Institute, Tairāwhiti/Gisborne,² Faculty of Medical and Health Sciences & Centre for Brain Research, University of Auckland, ³ Auckland Bioengineering Institute, University of Auckland,⁴ Tūranga Health, Tūranganui-a-kiwa, Tairāwhiti/Gisborne, New Zealand,⁵ Ngāti Porou, Ngāti Kahungunu, Rongomaiwahine, Rongowhakaata, Tairāwhiti/Gisborne,

⁶ Ngai Tāmanuhiri, Rongowhakaata, Ngāti Porou, Tairāwhiti/Gisborne, New Zealand, ⁷ General Electric Healthcare, Victoria, Australia, ⁸ Department of Engineering Science, Faculty of Engineering, University of Auckland.

Home

•

Project

•

Novel Subject-Specific Method of Visualising Group Differences from Multiple DTI Metrics without Averaging

Synopsis

Averaging is commonly used for data reduction/aggregation to summarise such high-dimensional data, resulting in information loss. However, individual variability makes group-wise comparisons difficult without data reduction/aggregation. To address these issues, we developed a novel technique that integrates diffusion tensor (DTI) metrics along the whole volumes of the Fibre bundle using a mesh-fitting technique. Using the right Corticospinal Tract (rCST) as an example, we demonstrate the utility of the method in detecting differences in DTI metrics of contact-sports and non-contact-sports athletes.

Introduction

Diffusion tensor MRI (DTI) generates four metrics (fractional anisotropy [FA], axial diffusivity [AD], radial diffusivity [RD], and mean diffusivity [MD]) per voxel, providing microstructural information about tissue. Averaging is commonly used for data reduction/aggregation to summarise such high-dimensional data, resulting in information loss. However, individual variability makes group-wise comparisons difficult without data reduction/aggregation. To address these issues, we developed a novel technique that integrates diffusion metrics along the whole volumes of the fibre bundle using a mesh-fitting technique. Since the right Corticospinal Tract (rCST) is known to be sensitive to brain injury⁽¹⁾, the utility of the method in detecting the differences in DTI metrics of contact-sports and non-contact-sports athletes is demonstrated using rCST.

Method

Participant information:
Under ethics approval, a cohort of contact-sports players (case, n=18) was imaged at 2 timepoints: preseason and postseason. Healthy non-contact-sports athletes from a matching demographic were imaged (control, n=9). Both cohorts were between 16-18 years old. Those with a history of severe brain injury or other neurological conditions were excluded.

Image Acquisition:
T1-weighted and DTI images (Table 1) were acquired on a 3T MRI scanner (SIGNA Premier; General Electric Healthcare, Milwaukee, WI; AIR™ 48-channel head coil).

DTI processing:
Image processing steps were performed using FSL (FMRIB software library) (http://fsl.fmrib.ox.ac.uk/fsl/, version 6.0)^{(2, 3, 4)}. Diffusion images were processed using FDT⁽⁵⁾.

An output with susceptibility-induced off-resonance field measure ^{(3, 6)}, was passed onto the eddy tool, which corrects eddy-current induced distortions and subject movements^(7). DTIFIT was used to generate the FA, MD, AD, and RD. To segment the rCST, linear registration (using FLIRT tool and MNI152_T1_1mm_brain atlas image ⁽⁸⁾ followed by a nonlinear registration (FNIRT) ⁽⁹⁾ was performed on T1-weighted images. Using the JHU ICBM-DTI-81 white-matter labels atlas ^(10-12), the rCST from the template space was wrapped back into T1-weighted native space. The diffusion metrics were extracted through rigid registration of the segmented rCST on the 3D tensor maps.

Embedding diffusion metrics in a 3D mesh via nonlinear morphing:
A high-fidelity 3D mesh template of the rCST comprising of hexahedral elements was developed from T1-weighted MRI. This template mesh was used to generate subject-specific meshes of rCST via Freeform deformation (FFD) of the template mesh onto the subject geometry. For each subject, the nodes on the external surfaces of the rCST template mesh were fitted to the geometry data points from the MRI segmentation while the internal nodes were transformed using the same deformation as the external nodes, preserving the relative nodal positions within the mesh (Figure 1).

This fitting method has been extensively used in subject-specific finite element model generation for the brain^{(13, 14),} knee, hip, and ankle joints^(15-17). After the fitting, the nearest voxel in the MRI space to each element was located using the nearest neighbour search algorithm in Python (Scipy cKDTree) ^{(13, 14)}. The average diffusion metrics value from the 9 nearest voxels were stored as field information for each node. Due to the use of common template mesh, the dimensionality of the DTI metric information is matched for all subjects, which is essential in performing the principal component analysis (PCA) step below.

Principal Component Analysis (PCA):
The pcaMethods library from R statistical software (version 4.1.2) was used to perform PCA. The normalised and scaled values of FA, MD, AD, and RD from each element (total n=20,480) of the fitted mesh were used to generate independent, linear combinations for each individual. Plots of PCA components 1 and 2 were then used to visualise clustering of cases vs. controls, based on the individual variance in the rCST.

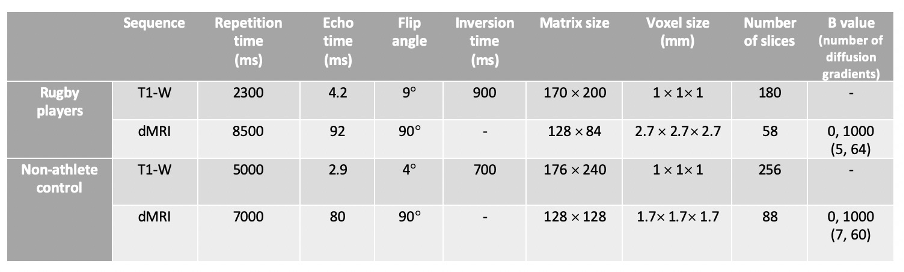
Table 1: Acquisition parameters for the T1- weighted and diffusion tensor (DTI) sequence.

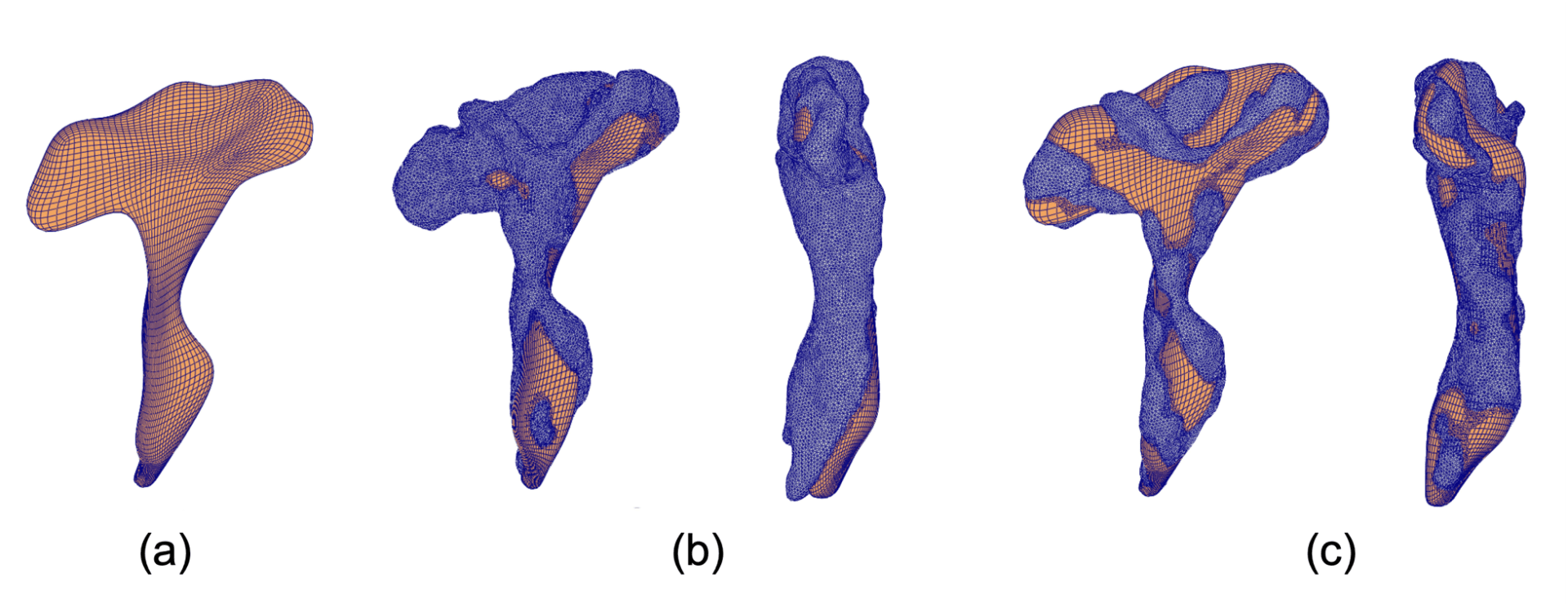
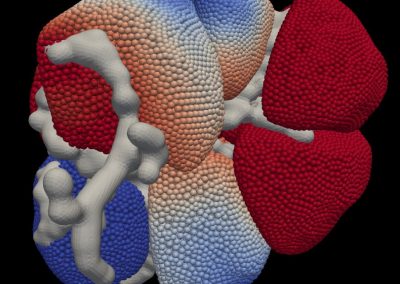
Figure 1: How subject-specific mesh fitting is performed. Free form deformation process that morphs a template mesh to a new subject’s geometry. (a) Template mesh created from a subject to roughly resemble the generic shape of the rCST. (b) 20,480 squares are overlaid on each specific subject’s geometry. Since the match is not optimized for each subject, the template mesh is deformed to minimize the rms error. (c) The optimized subject-specific fitted mesh. Both coronal and sagittal view are shown for (b) and (c).

Results

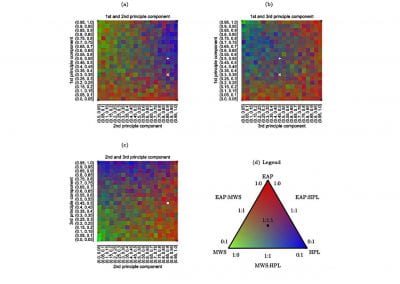
As shown in Figure 2, the diffusion values of each cohort could be statistically summarised to show the variation between ±2 standard deviations for the entire rCST due to the matched dimensionality. Figure 3 shows clustering PCA dimensions PC1 and PC2 (accounting from 33% (FA) to 47% (RD) of the data variation) which allowed for the discrimination between case vs. controls based on the major variance in the DTI measurements from each element of the rCST model

Discussion

A novel approach is introduced for investigating the brain’s white matter tracts by combining different techniques from different disciplines – that is, DTI analysis from MRI; mesh fitting from computer graphics; and PCA from statistical data analysis. By generating the 3D template mesh model of the right corticospinal tract (known to be sensitive to brain injury⁽¹⁾ and morphing it into each subject’s native space, we made a subject-specific model for the tract that matched both the geometry and diffusion metrics distribution.

The method extracts the diffusion metrics corresponding to regions with minimal information loss. The common dimension of the 20,480 diffusion metrics allowed further data aggregation using PCA to cluster the case and control groups.

Conclusion

The work presents a novel method that accounts for the individual subject’s geometric variation, to visualise group differences in quantitative MR data. By embedding tensor-based data from DTI scans to 3D subject-specific mesh, we showed the ability of our model to separate alterations in image-based metrics acquired from contact sports players and non-contact-sports athletes. Future prediction models based on other quantitative MRI methods may benefit from this approach.

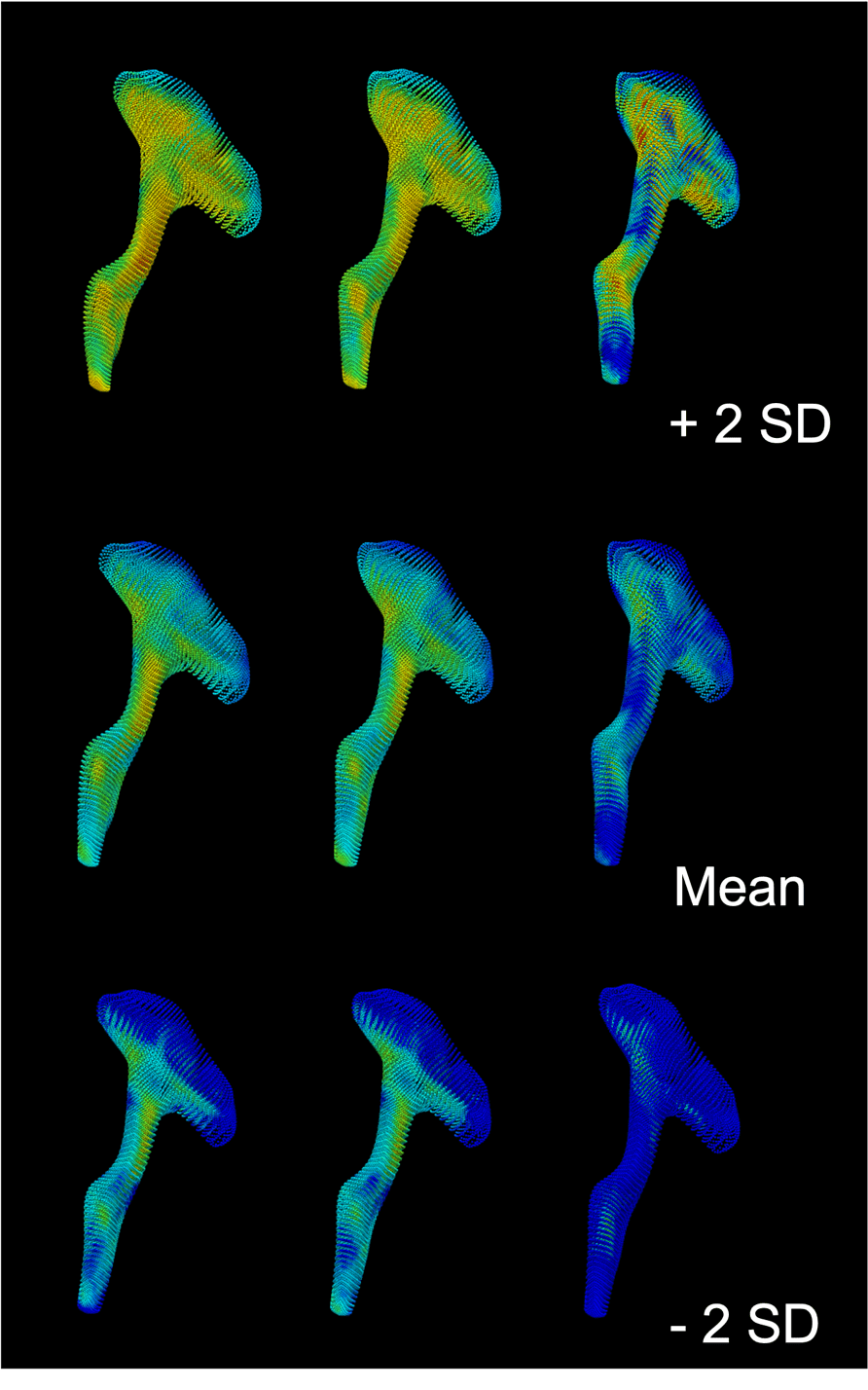
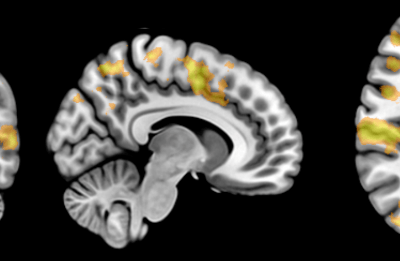
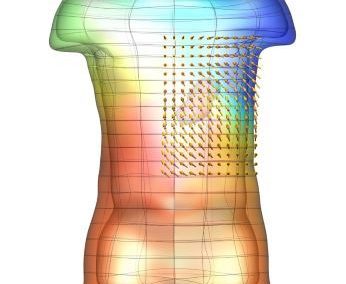
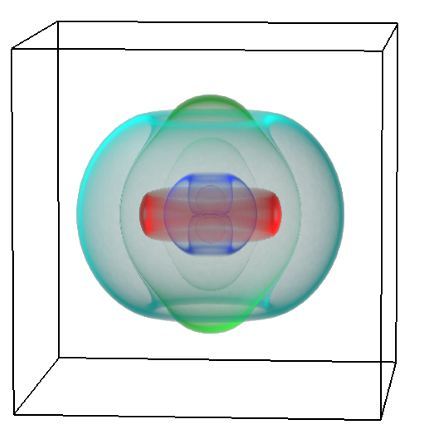
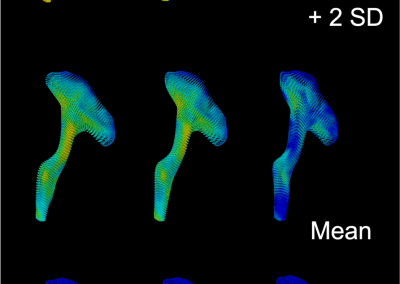
Figure 2: How group average values can be visualized based on the subject-specific mesh fitting result. rCST tract FA value visualisation showing different group mean and ±2 standard deviations of the preseason (left), postseason (middle), and control (right) cohorts

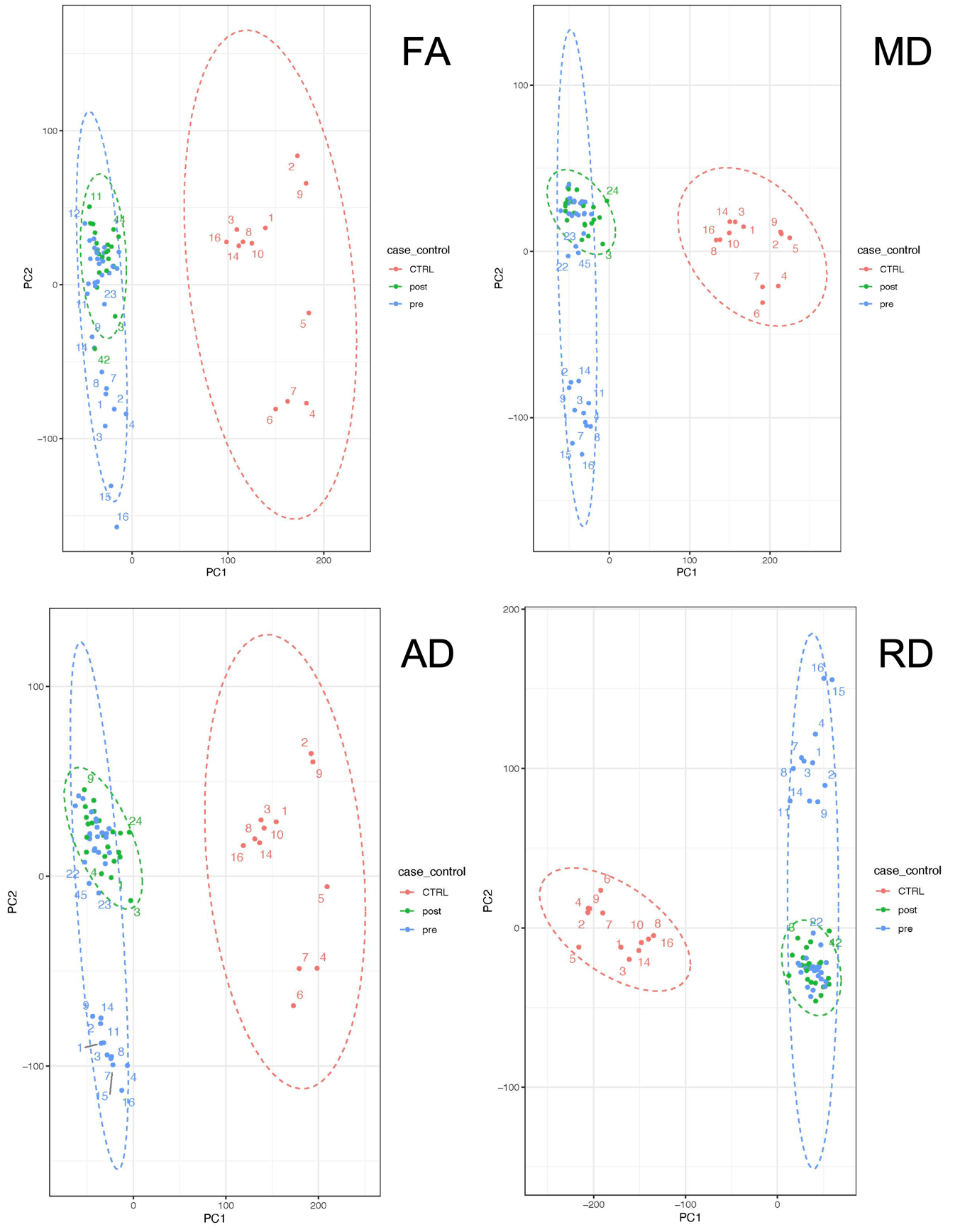
Figure 3: Principal components 1 and 2 shows the clustering of the case and control for each diffusion variable FA (Fractional anisotropy), MD (Mean diffusivity), AD (Axial Diffusivity), RD (Radial Diffusivity).

References

Asken BM, DeKosky, S.T., Clugston, J.R. et al. Diffusion tensor imaging (DTI) findings in adult civilian, military, and sport-related mild traumatic brain injury (mTBI): a systematic critical review. Brain Imaging and Behavior 12, 585–612 (2018).
Woolrich MW, Jbabdi S, Patenaude B, Chappell M, Makni S, Behrens T, et al. Bayesian analysis of neuroimaging data in FSL. NeuroImage. 2009;45(1 Suppl):S173-86.
Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, et al. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage. 2004;23 Suppl 1:S208-19.
Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM. FSL. NeuroImage. 2012;62(2):782-90.
Behrens TE, Woolrich MW, Jenkinson M, Johansen-Berg H, Nunes RG, Clare S, et al. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn Reson Med. 2003;50(5):1077- 88.
Andersson JL, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echoplanar images: application to diffusion tensor imaging. NeuroImage. 2003;20(2):870-88.
Andersson JLR, Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage. 2016;125:1063-78.
Jenkinson M, Bannister P, Brady M, Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage. 2002;17(2):825-41.
Jesper L. R. Andersson MJaSS. Non-linear registration aka Spatial normalisation. Oxford, United Kingdom: FMRIB Centre; 2007
Wakana S, Caprihan A, Panzenboeck MM, Fallon JH, Perry M, Gollub RL, et al. Reproducibility of quantitative tractography methods applied to cerebral white matter. NeuroImage. 2007;36(3):630-44.
Hua K, Zhang J, Wakana S, Jiang H, Li X, Reich DS, et al. Tract probability maps in stereotaxic spaces: analyses of white matter anatomy and tract-speciYc quantification. NeuroImage. 2008;39(1):336-47.
Mori S, Oishi K, Faria A V, M ZPC. MRI Atlas of Human White Matter. Amsterdam, The Netherlands: Elsevier; 2005.
Shim VB, Tayebi M, Kwon E, Guild S, Scadeng M, Dubowitz D, Mcbryde F, Rosset S, Wang A, Fernandez JW, Li S, Holdsworth S. Combining advanced magnetic resonance imaging (MRI) with Ynite element (FE) analysis for characterising subject-specific injury patterns in the brain after traumatic brain injury. Engineering with Computers. 2022.
Shim VB, Holdsworth S, Champagne AA, Coverdale NS, Cook DJ, Lee TR, et al. Rapid Prediction of Brain Injury Pattern in mTBI by Combining FE Analysis With a Machine-Learning Based Approach. IEEE Access. 2020;8:179457-65.
Shim VB, Fernandez JW, Gamage PB, Regnery C, Smith DW, Gardiner BS, et al. Subject-specific finite element analysis to characterize the influence of geometry and material properties in Achilles tendon rupture. J Biomech. 2014;47(15):3598- 604.
Munro JT, Millar JS, Fernandez JW, Walker CG, Howie DW, Shim VB. Risk analysis of patients with an osteolytic acetabular defect after total hip arthroplasty using subject-specific finite-element modelling. Bone Joint J. 2018;100-b(11):1455-62.
Shim VB, Besier TF, Lloyd DG, Mithraratne K, Fernandez JF. The influence and biomechanical role of cartilage split line pattern on tibiofemoral cartilage stress distribution during the stance phase of gait. Biomech Model Mechanobiol. 2016;15(1):195-204.