Number theoretic algorithms in cryptography
Shi Bai, Steven D. Galbraith, Department of Mathematics
Modern public-key cryptography is about communication in the presence of adversaries, allowing users to communicate confidentially without requiring a secret key to be distributed by a trusted party in advance [1]. The security of public-key cryptosystems is usually based on the presumed hardness of certain number- theoretical problems such as integer factorization and lattice problems. Therefore, it is important to understand the difficulties (both theoretical and practical) of the underlying computational problems. The project aims to understand the security of modern cryptosystems by investigating the computational efforts that are required to attack them.
Our main goal therefore is to investigate new and improved algorithms for solving certain important computational problems. The NeSI Pan high performance cluster provides significant computational power and parallel scalability for us to investigate these algorithms. Our research has practical importance for the security of modern cryptosystems: suggesting safe parameters for them as well as constructing new schemes and protocols.
Schemes
There are two scenarios in the scope of our research: pre-quantum and post-quantum cryptosystems. At present, many public-key cryptosystems rely on the presumed hardness of integer factorization and computing discrete logarithms. Such cryptosystems are often referred-to as the pre-quantum schemes as there exist efficient algorithms to attack them on quantum computers. In contrast, new mathematical foundations for cryptography such as lattices are becoming interesting as they can be used to construct post-quantum cryptosystems (since they are believed to be secure even against attackers with quantum computers).
Integer factorization
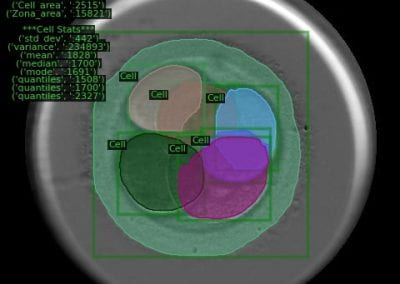
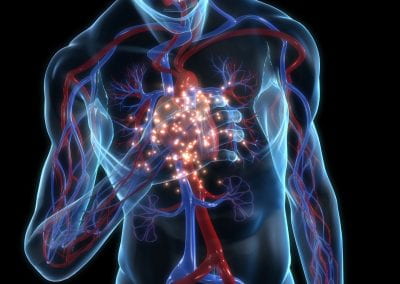
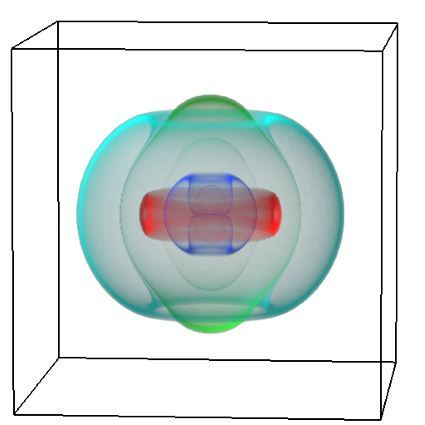
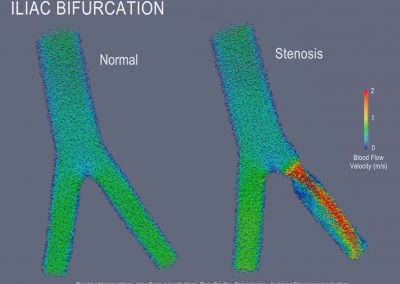
The first scenario is concerning the factorization of large integers. The RSA cryptosystem relies on the assumed difficulty of the large integer factorization problem. Figure 1 shows the RSA-1024 challenge, a 309-decimal digit number, which has not been factored so far. The number field sieve (NFS) is asymptotically the most efficient algorithm known for factoring large integers. Its time complexity is sub-exponential. It consists of several stages, the first one being polynomial selection. The running time of NFS depends on the quality of the polynomials. The project aims to investigate efficient algorithms for polynomial selection. The NeSI Pan cluster provides computational resources for the project, as the computational requirements of such a computation are substantial. For large integer factorization, a few thousand jobs are usually running on the cluster at a time. Such tasks would not be possible to accomplish without the usage of the NeSI cluster.

Figure 1 RSA-1024
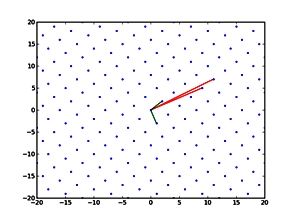
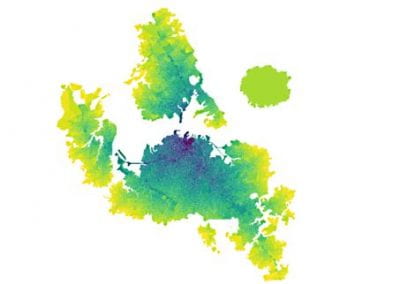
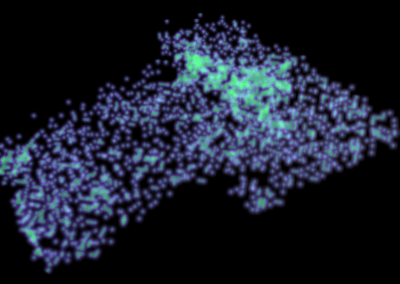
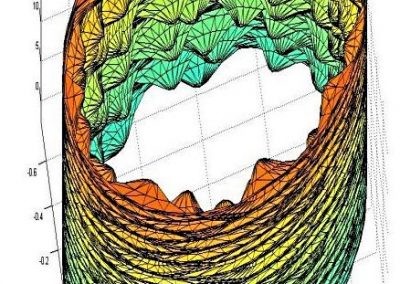
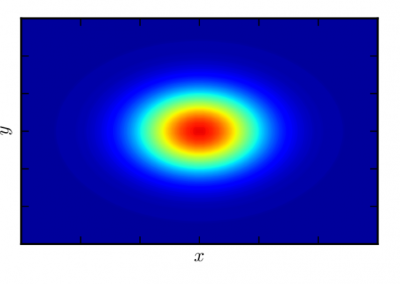
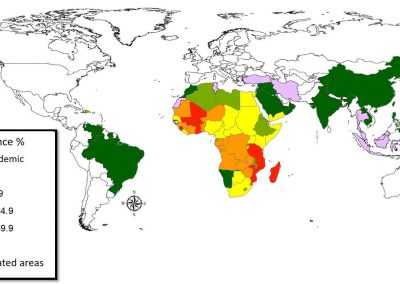
Figure 2: Two bases in a 2-dimensional lattice
Lattice-based cryptosystems
The second scenario is to study the computational hardness of certain lattice problems. A lattice can be visualized as a periodic arrangement of points in space (Figure 2). The difficulty is that there are many different ways to write down a “basis” for a lattice.Lattice- based cryptosystems often rely on the assumed difficulty of finding certain vectors that satisfy nice properties (e.g. shortness) in a lattice. At present, lattice-based cryptosystems have relatively large keys and/or ciphertext size compared to traditional cryptosystems such as RSA. Hence, an important research problem in lattice-based cryptography is to obtain practical public key schemes that are still provably secure under lattice assumptions. The NeSI cluster helps us to investigate the security of lattice-based systems through large- scale computation.
Real-world application
The research has practical implications for the real world, as cryptography is critical for electronic transactions everywhere, such as e-mail, e-commerce and mobile communications. It is important to make sure the cryptographic algorithms are secure and efficient. One of our research outputs helps to build more efficient and provably secure digital signatures on lattices (e.g. [3]). Our research also helps us identify potential vulnerabilities and weaknesses of cryptographic algorithms and hence suggest safe parameters and constructions for crypto-protocols [2]. For example, researcher Zachary Harris used our software cado-nfs to find vulnerability in Google [5] (using a too small RSA key for email authentication). Recently, two researchers Fabien Perigaud and Cedric Pernet from the Cassidian Cybersecurity used our software cado-nfs to reverse- engineer a ransomware[6].
Network and collaboration
We are participating in international collaborative research projects that bring together researchers from France, Germany, USA and other countries. We have been involved in co-developing the open-source software cado-nfs (http://cado-nfs.gforge.inria.fr), which has been used in the computation on the Pan cluster. We hope to attack some large-scale computational problems in feasible time through our collaboration. Locally, our research, computation and experiments would not have been possible without access to the NeSI computing facilities and help from the Centre of eResearch staff.
References
- Ronald L. Rivest. Cryptography. Handbook of Theoretical Computer Science. J. Van Leeuwen (ed.),
- Shi Bai and Steven D. Galbraith. Lattice decoding attacks on binary LWE. ACISP, Lecture Notes in Computer Science, 8544, 2014.
- Shi Bai and Steven D. Galbraith. An improved compression technique for signatures based on learning with errors. In J. Benaloh (Ed.), CT-RSA 2014, LNCS 8366 (2014) 28–47.
- Shi Bai, Richard Brent and Emmanuel Thome. Root optimization of polynomials in the number field sieve. Mathematics of Computation,
- Zachary Harris, How a Google Headhunter’s E-Mail Unraveled a Massive Net Security Hole, http://www.wired.com/2012/10/ dkim-vulnerability-widespread.
- Fabien Perigaud, Cedric Pernet, Bitcrypt broken, http://blog.com/post/2014/02/Bitcrypt-broken.
See more case study projects

Our Voices: using innovative techniques to collect, analyse and amplify the lived experiences of young people in Aotearoa
Painting the brain: multiplexed tissue labelling of human brain tissue to facilitate discoveries in neuroanatomy

Detecting anomalous matches in professional sports: a novel approach using advanced anomaly detection techniques
Benefits of linking routine medical records to the GUiNZ longitudinal birth cohort: Childhood injury predictors
Using a virtual machine-based machine learning algorithm to obtain comprehensive behavioural information in an in vivo Alzheimer’s disease model
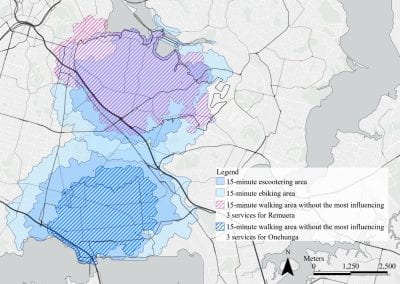
Mapping livability: the “15-minute city” concept for car-dependent districts in Auckland, New Zealand
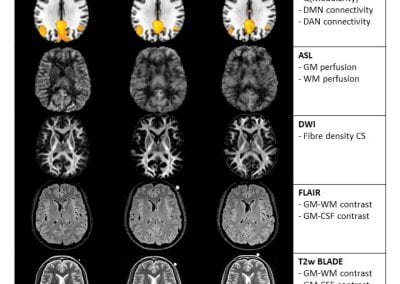
Travelling Heads – Measuring Reproducibility and Repeatability of Magnetic Resonance Imaging in Dementia
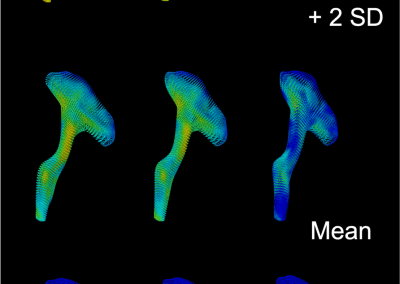
Novel Subject-Specific Method of Visualising Group Differences from Multiple DTI Metrics without Averaging

Re-assess urban spaces under COVID-19 impact: sensing Auckland social ‘hotspots’ with mobile location data
Aotearoa New Zealand’s changing coastline – Resilience to Nature’s Challenges (National Science Challenge)
Proteins under a computational microscope: designing in-silico strategies to understand and develop molecular functionalities in Life Sciences and Engineering
Coastal image classification and nalysis based on convolutional neural betworks and pattern recognition
Determinants of translation efficiency in the evolutionarily-divergent protist Trichomonas vaginalis
Measuring impact of entrepreneurship activities on students’ mindset, capabilities and entrepreneurial intentions

Using Zebra Finch data and deep learning classification to identify individual bird calls from audio recordings
Automated measurement of intracranial cerebrospinal fluid volume and outcome after endovascular thrombectomy for ischemic stroke

Using simple models to explore complex dynamics: A case study of macomona liliana (wedge-shell) and nutrient variations
Fully coupled thermo-hydro-mechanical modelling of permeability enhancement by the finite element method

Modelling dual reflux pressure swing adsorption (DR-PSA) units for gas separation in natural gas processing
Molecular phylogenetics uses genetic data to reconstruct the evolutionary history of individuals, populations or species
Wandering around the molecular landscape: embracing virtual reality as a research showcasing outreach and teaching tool