Studying the shape and the size of the universe
Grigor Aslanyan, Department of Physics
Data from spacecraft helps refine theoretical models of the universe
The study of the universe as a whole goes back to as early as 1915 when Einstein introduced General Relativity. Only two years later, Willem de Sitter realized that General Relativity did not predict or constrain the global shape of the universe. There is no theoretical reason to believe that the universe is infinite. In fact, certain theoretical arguments about the birth of the universe give preference to finite non-trivial shapes such as a 3-torus (A. Linde, 2004). This subject remained purely speculative until very recent accurate measurements of the cosmic microwave background (CMB) anisotropies were made by the Cosmic Background Explorer (COBE) satellite (launched in 1989) and the Wilkinson Microwave Anisotropy Probe (WMAP) spacecraft (launched in 2001).
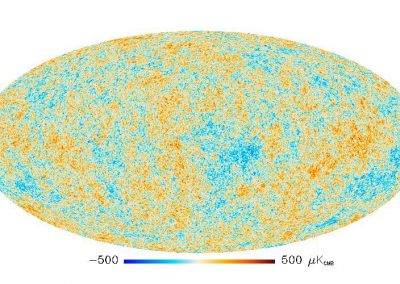
The CMB was emitted very shortly after the big bang so it gives a snapshot of the very early universe. A non-trivial shape of the universe changes the pattern of the CMB in certain ways which makes CMB an excellent tool to study the global properties of the universe. Several groups have addressed the problem before some of which found a slight preference for a finite rather than infinite shape of the universe. However, studying the statistical significance of the results (i.e., what the probability is that the universe has a non-trivial shape) is computationally challenging and certain approximations need to be used.
My research studying the shape and size of the universe involves doing a precise statistical analysis of three different shapes of the universe with the most recent data from WMAP (Figure 1) and testing the approximations used in previous studies. Moreover, the Planck satellite which was launched in 2009 is expected in 2014 to deliver precise measurements of the polarisation of CMB. This essentially will double the amount of data currently available and can greatly improve our understanding of the shape of the universe. For the first time my colleagues and I developed the formalism to include the polarization data in the analysis. We then used simulations to predict how far the polarisation data from the Planck satellite can push the current limits on the shape and the size of the universe.
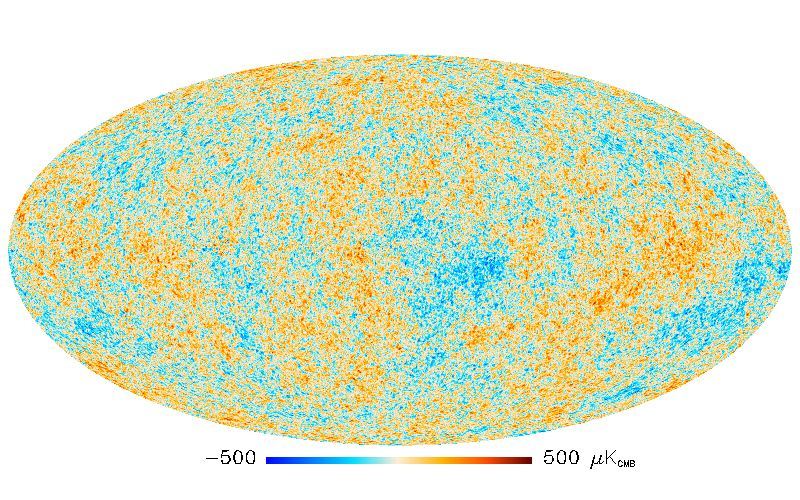
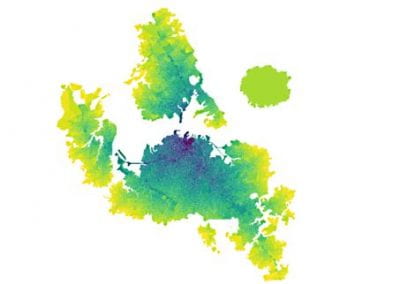
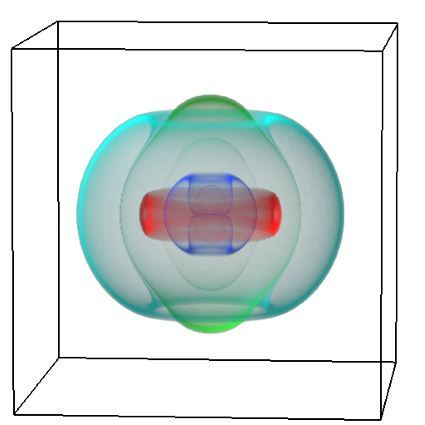
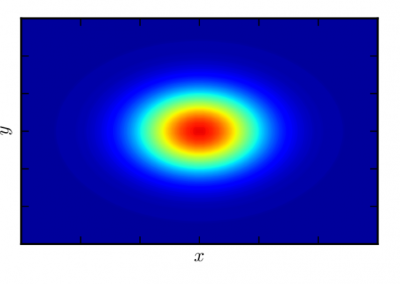
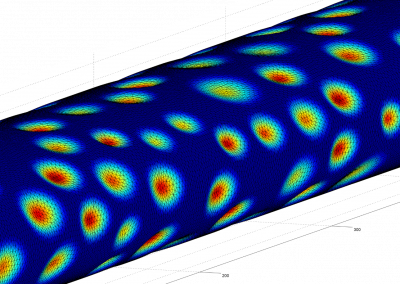
Figure 1: The temperature anisotropies of the cosmic microwave background from the final release of WMAP data.

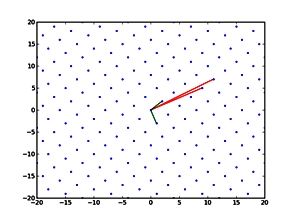
Figure 2: A torus in two dimensions
The shapes we studied are that of the torus in 1, 2, and 3 dimensions. These are among the most popular theoretical candidates. A torus in 1 dimension is simply a circle (the other two dimensions are infinite). If one travels in that direction she will eventually come back to the starting point. A 2-dimensional torus has the shape of a donut (the third dimension is infinite) (Figure 2). It is impossible to draw a torus in 3-dimensions, but it is a simple generalisation of the previous cases. One can imagine it as a cube with opposite edges identified; i.e. if one hits the edge of the cube she simply enters the cube from the opposite side. Our results were recently published in JCAP 08 (2013) 009, also available on arXiv, 1304.1811. They indicate that certain approximations used in previous studies tend to overestimate the statistical significance of a detection of non-trivial shapes. Simulations are crucial to accurately estimate the implications of the data about the shape and the size of the universe. It can also predict with high significance a torus topology with a size even bigger than the observable part of the universe. The techniques we have developed can be used with the actual data once it is released. The results could provide a very important piece of information about the connection between quantum physics and General Relativity and how the universe emerged from the quantum foam of spacetime.
Simulating the size and shape of the universe
Many simulations of the shape and size of the universe were needed to accurately estimate the statistical significance of the possible detection from the real experimental data. If the universe has a non-trivial shape then it must have a certain size and orientation. One needs to simulate data with all possible sizes and orientations with a sufficiently small step size. In order to obtain accurate results, on the Pan cluster we simulated 500 skies for 25 different sizes of the three topologies analysed – about 40,000 simulations in total. For each simulation we had to do a detailed fit with all possible orientations. As our results confirmed, doing this analysis was very important in order to find accurate results. This task would not be possible to accomplish without the usage of the Pan cluster. Each simulation could be analysed independently so it was very easy to use parallel computation. We were able to run many simulations on different cores of the cluster at the same time which significantly increased the speed of the analysis.
The most important next step will be to analyse the actual polarisation data from the Planck satellite when it becomes available in 2014. Another important future study would be to analyse a torus topology allowing all 3 sides to have different lengths. Unfortunately, this is computationally much more demanding than our current study, and even the usage of the Pan cluster would not help accomplish the task with the same techniques. One needs to come up with a different theoretical approach for that analysis, and this is one interesting and important study for the future.
See more case study projects

Our Voices: using innovative techniques to collect, analyse and amplify the lived experiences of young people in Aotearoa
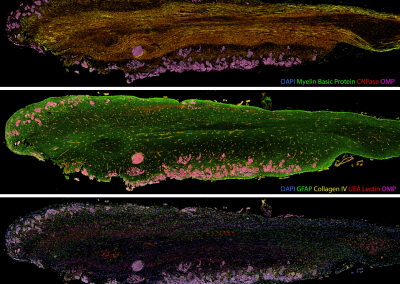
Painting the brain: multiplexed tissue labelling of human brain tissue to facilitate discoveries in neuroanatomy

Detecting anomalous matches in professional sports: a novel approach using advanced anomaly detection techniques
Benefits of linking routine medical records to the GUiNZ longitudinal birth cohort: Childhood injury predictors
Using a virtual machine-based machine learning algorithm to obtain comprehensive behavioural information in an in vivo Alzheimer’s disease model
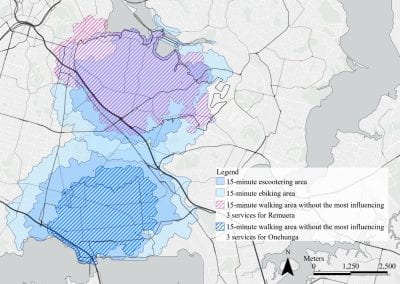
Mapping livability: the “15-minute city” concept for car-dependent districts in Auckland, New Zealand
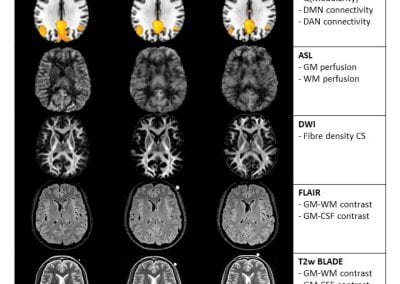
Travelling Heads – Measuring Reproducibility and Repeatability of Magnetic Resonance Imaging in Dementia
Novel Subject-Specific Method of Visualising Group Differences from Multiple DTI Metrics without Averaging

Re-assess urban spaces under COVID-19 impact: sensing Auckland social ‘hotspots’ with mobile location data
Aotearoa New Zealand’s changing coastline – Resilience to Nature’s Challenges (National Science Challenge)
Proteins under a computational microscope: designing in-silico strategies to understand and develop molecular functionalities in Life Sciences and Engineering
Coastal image classification and nalysis based on convolutional neural betworks and pattern recognition
Determinants of translation efficiency in the evolutionarily-divergent protist Trichomonas vaginalis
Measuring impact of entrepreneurship activities on students’ mindset, capabilities and entrepreneurial intentions

Using Zebra Finch data and deep learning classification to identify individual bird calls from audio recordings
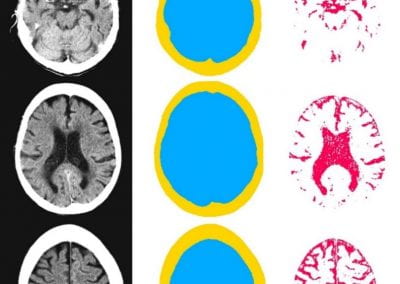
Automated measurement of intracranial cerebrospinal fluid volume and outcome after endovascular thrombectomy for ischemic stroke

Using simple models to explore complex dynamics: A case study of macomona liliana (wedge-shell) and nutrient variations
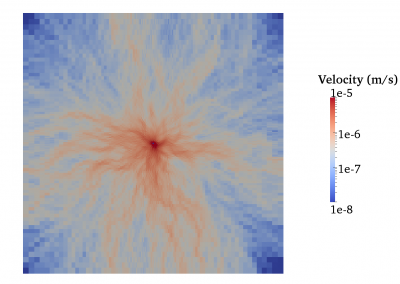
Fully coupled thermo-hydro-mechanical modelling of permeability enhancement by the finite element method

Modelling dual reflux pressure swing adsorption (DR-PSA) units for gas separation in natural gas processing
Molecular phylogenetics uses genetic data to reconstruct the evolutionary history of individuals, populations or species
Wandering around the molecular landscape: embracing virtual reality as a research showcasing outreach and teaching tool